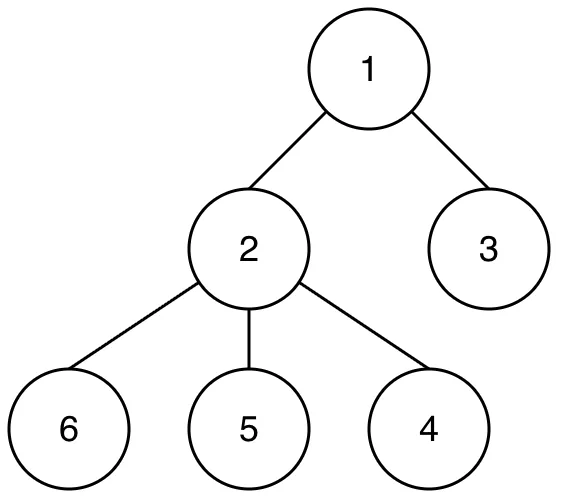
Tree?
트리는 데이터를 계층적으로 표현하는 자료구조 입니다. 생긴게 나무를 뒤집어 놓은것 같이 생겨서 트리라는 이름이 붙여졌습니다.
용어 정리
우선 트리에서 쓰이는 용어 먼저 정리하겠습니다.
- 노드(Node): 트리를 구성하는 기본 요소입니다.
- 루트(Root): 부모 노드가 존재하지 않는 트리의 시작점 입니다.
- 부모(Parent): 자식을 가진 노드입니다.
- 자식(Child): 부모 노드에 연결된 하위 노드입니다.
- 형제(Sibling): 같은 부모를 가진 노드입니다.
- 리프(Leaf): 자식이 없는 노드입니다.
- 깊이(Depth): 루트 노드에서 어떤 노드까지 도달하는데 거치는 간선의 개수입니다.
- 높이(Height): 가장 깊은 리프 노드의 깊이입니다.
- 차수(Degree): 한 노드가 가지는 자식의 개수입니다.
트리 특징
- 트리는 사이클이 없습니다. 만약 사이클이 있다면 그래프라고 분류됩니다.
- 루트 노드는 무조건 1개입니다.
- 노드 개수가 N개라면, 간선의 개수는 반드시 N-1개 입니다.
- 트리의 자식도 트리이고, 그 자식도 트리입니다.
그래프 유형
일반 트리
자식 노드 개수에 제한이 없는 일반적인 트리입니다.
이진 트리
모든 노드의 차수가 최대 2인 트리입니다.
모든 노드가 꽉찬 이진 트리를 포화 이진 트리, 위에서 아래, 왼쪽에서 오른쪽 순서대로 채워진 트리를 완전 이진 트리라고 합니다.
이진 탐색 트리
왼쪽 자식 < 부모 < 오른쪽 자식 순으로 정렬된 트리입니다.
이 외에도 AVL tree, B-Tree 등 다양한 트리 변형이 있습니다.
동작 원리
BST(이진 탐색 트리)를 기준으로 C로 구현한 예제와 함께 설명하겠습니다.
구조체 선언
1
2
3
4
5
typedef struct Node {
int key;
struct Node* left;
struct Node* right;
};
이진트리의 구조체는 간단합니다. 자식은 좌우 각각 하나씩 최대 2개만 가질 수 있기 때문에 자식 노드를 표기할 포인터와 노드 자체의 값을 표현하는 key만 있으면 됩니다.
탐색
1
2
3
4
5
6
7
Node* search(Node* node, int key) {
if (node == NULL) return NULL;
if (node->key == key) return node;
if (node->key > key) return search(node->left, key);
return search(node->right, key);
}
탐색은 찾으려는 값이 현재 노드의 키보다 작으면 왼쪽, 아니면 오른쪽 자식을 재귀적으로 탐색합니다. 노드의 키와 찾으려는 키가 같으면 탐색을 중단하고 해당 노드를 리턴합니다.
삽입
1
2
3
4
5
6
7
8
Node* insert(Node* node, int key) {
if (node == NULL) return createNode(key);
if (node->key > key) node->left = insert(node->left, key);
if (node->key < key) node->right = insert(node->right, key);
return node;
}
BST는 노드의 키보다 작은 값은 왼쪽 자식으로, 노드의 키보다 큰 값은 오른쪽 자식으로 삽입합니다. 노드의 키와 삽입할 값을 재귀적으로 비교해서 리프노드까지 도달한 후, 리프 노드에서도 같은 과정을 통해 값을 추가합니다.
삭제
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
Node* findMinNode(Node* node) {
Node* current = node;
while (current && current->left != NULL) {
current = current->left;
}
return current;
}
Node* delete(Node* node, int key) {
if (node == NULL) return NULL;
if (node->key > key) node->left = delete(node->left, key);
if (node->key < key) node->right = delete(node->right, key);
Node* temp = NULL;
if (node->left == NULL) {
temp = node->right;
free(node);
return temp;
}
if (node->right == NULL) {
temp = node->left;
free(node);
return temp;
}
temp = findMinNode(node->right);
node->key = temp->key;
node->right = delete(node->right, temp->key);
return node;
}
삭제는 세 가지 경우를 고려해야 합니다.
자식이 없는 리프 노드일 때
그냥 삭제하면 됩니다.
자식이 하나만 있는 노드일 때
자신의 자식을 부모 노드의 자식으로 변경 후 삭제하면 됩니다.
자식이 둘 다 있을 때
오른쪽 자식중 가장 작은 값을 찾아 대상 노드에 반영하고, 찾은 값은 지웁니다.
순회
노드를 순차적으로 방문하는 과정을 순회라고 합니다.
전위순회 (Pre-order)
1
2
3
4
5
6
void preorder(Node* node) {
if (node == NULL) return;
printf("%d ", node->key);
preorder(node->left);
preorder(node->right);
}
부모-좌-우 순서로 방문하는 순회입니다. 트리의 구조를 그대로 표현할 때 사용됩니다.
중위순회 (In-order)
1
2
3
4
5
6
void inorder(Node* node) {
if (node == NULL) return;
inorder(node->left);
printf("%d ", node->key);
inorder(node->right);
}
좌-부모-우 순서로 방문하는 순회입니다. BST에서는 오름차순된 값을 얻을 수 있습니다.
후위순회 (Post-order)
1
2
3
4
5
6
void postorder(Node* node) {
if (node == NULL) return;
postorder(node->left);
postorder(node->right);
printf("%d ", node->key);
}
좌-우-부모 순서로 방문하는 순회입니다. 트리 삭제에 사용되는 순회입니다.
전체 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
// BST
typedef struct Node {
int key;
struct Node* left;
struct Node* right;
} Node;
Node* createNode(int key) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->key = key;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
Node* search(Node* node, int key) {
if (node == NULL) return NULL;
if (node->key == key) return node;
if (node->key > key) return search(node->left, key);
return search(node->right, key);
}
Node* insert(Node* node, int key) {
if (node == NULL) return createNode(key);
if (node->key > key) node->left = insert(node->left, key);
if (node->key < key) node->right = insert(node->right, key);
return node;
}
Node* findMinNode(Node* node) {
Node* current = node;
while (current && current->left != NULL) {
current = current->left;
}
return current;
}
Node* delete(Node* node, int key) {
if (node == NULL) return NULL;
if (node->key > key) node->left = delete(node->left, key);
if (node->key < key) node->right = delete(node->right, key);
Node* temp = NULL;
if (node->left == NULL) {
temp = node->right;
free(node);
return temp;
}
if (node->right == NULL) {
temp = node->left;
free(node);
return temp;
}
temp = findMinNode(node->right);
node->key = temp->key;
node->right = delete(node->right, temp->key);
return node;
}
void preorder(Node* node) {
if (node == NULL) return;
printf("%d ", node->key);
preorder(node->left);
preorder(node->right);
}
void inorder(Node* node) {
if (node == NULL) return;
inorder(node->left);
printf("%d ", node->key);
inorder(node->right);
}
void postorder(Node* node) {
if (node == NULL) return;
postorder(node->left);
postorder(node->right);
printf("%d ", node->key);
}
int main() {
Node* root = NULL;
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
printf("preorder: ");
preorder(root);
printf("\n\n");
printf("inorder: ");
inorder(root);
printf("\n\n");
printf("postorder: ");
postorder(root);
printf("\n\n");
printf("search 40\n");
Node* found = search(root, 40);
if (found) printf("success %d\n\n", found->key);
else printf("not found\n\n");
printf("delete 50\n");
root = delete(root, 50);
printf("inorder: ");
inorder(root);
printf("\n\n");
return 0;
}