개요
백준애 19277 - ADD, DIV, MAX 문제를 풀고 신선한 충격을 받아 풀이를 정리해보려고 합니다. 해당 문제는 세그먼트 트리 비츠 라는 자료구조가 사용되었는데, 이 알고리즘을 이해하려면 세그먼트 트리, 레이지 세그먼트 트리의 이해가 선행되어야 합니다. 그래서 오늘을 세그먼트 트리에 대해서 정리헤 보겠습니다.
세그먼트 트리?
세그먼트 트리는 연속된 데이터 리스트에서 구간합을 구할때 일반적인 선형적인 방법보다 빠르게 구할 수 있는 자료구조 입니다. 세그먼트 트리는 이진트리를 활용하여 구간합을 저장하는 방식으로 빠른 구간합 탐색이 가능하게 합니다. 예제와 함께 자세히 동작 방식을 알아보겠습니다.
초기화
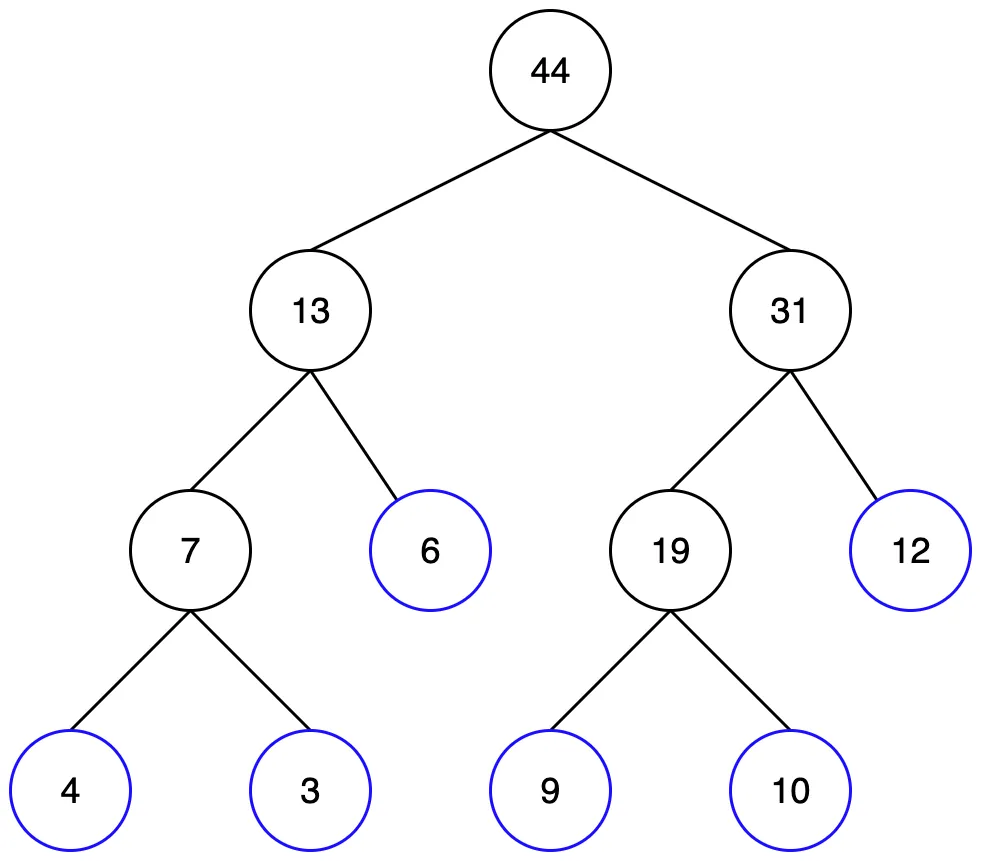
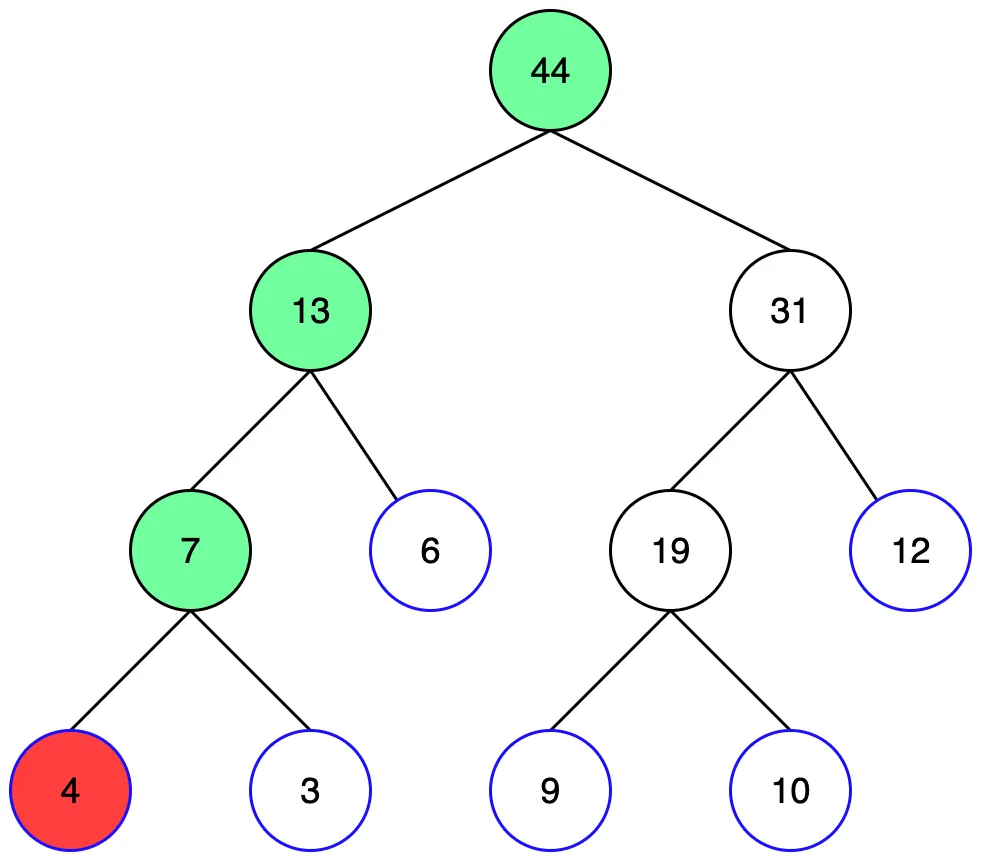
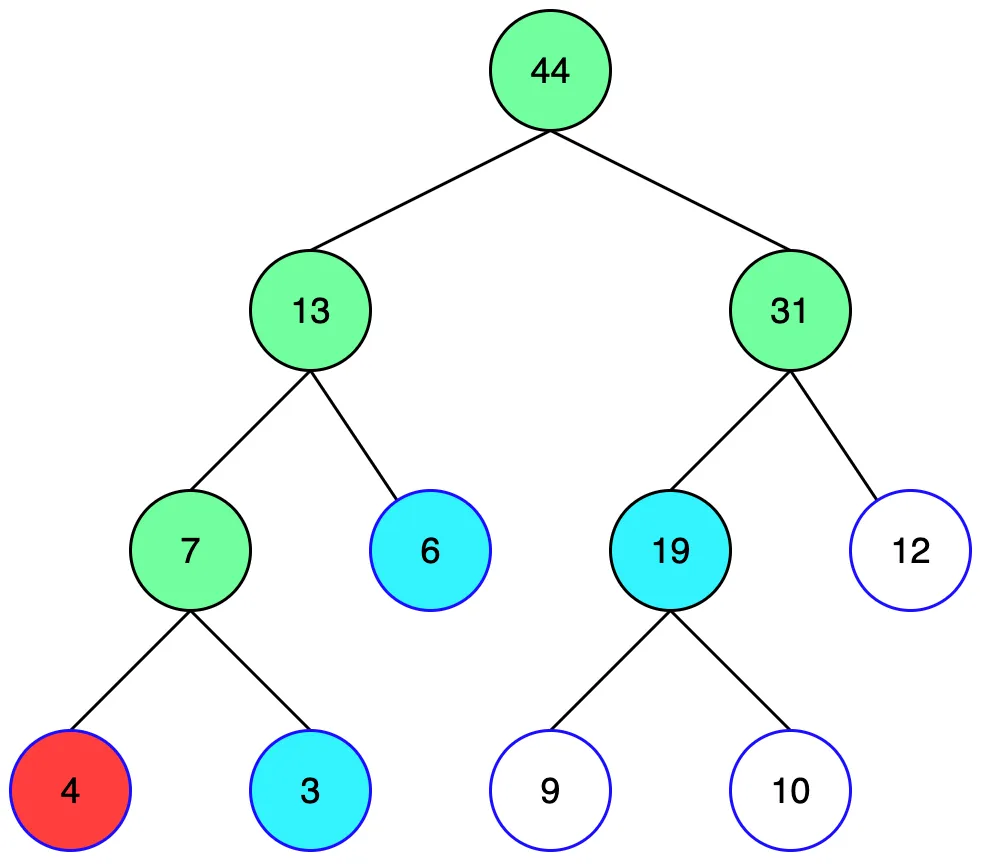
[4, 3, 6, 9, 10, 12] 6개의 숫자 리스트를 예제로 살펴보겠습니다.
그림에서 파란색으로 표시된 리프노드에 기존 데이터 리스트의 아이템이 순서대로 배치되고, 각 노드의 부모 노드는 자식 노드의 합이 저장됩니다. 초기화 과정을 코드로 구현하면 다음과 같습니다.
1
2
3
4
5
6
def init(node, left, right):
if left == right:
tree[node] = data[left - 1]
return tree[node]
mid = (left + right) // 2
tree[node] = init(node * 2, left, mid) + init(node * 2 + 1, mid + 1, right)
쿼리
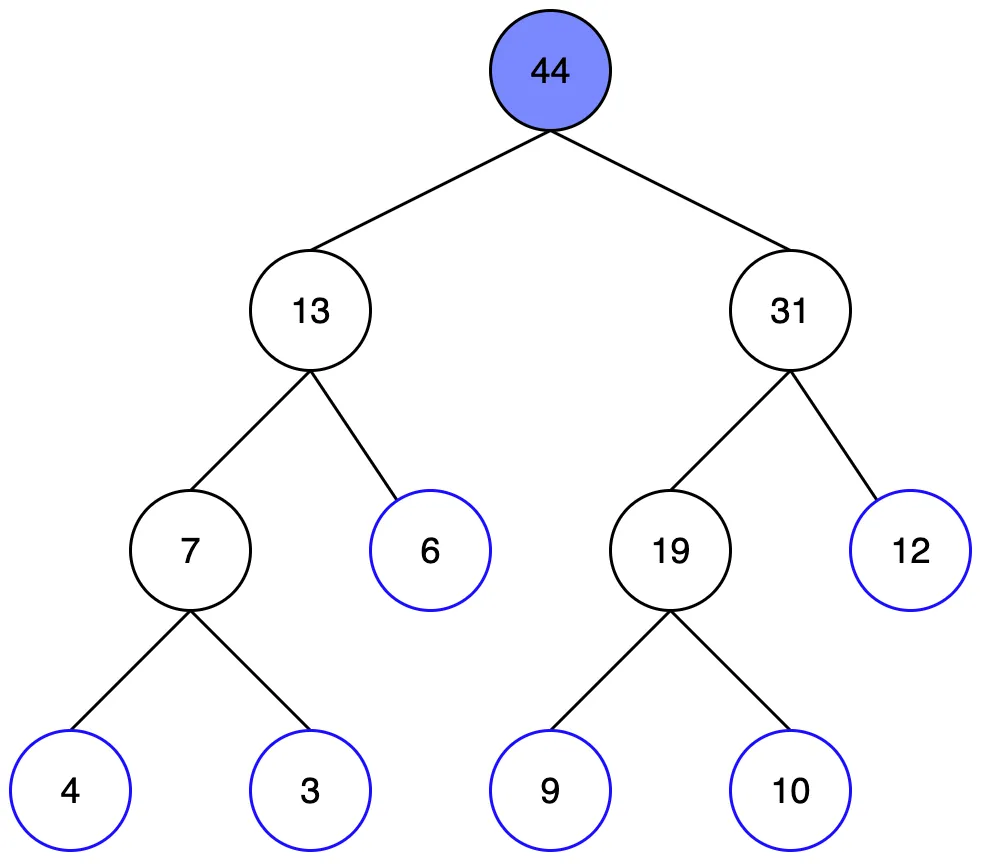
세그먼트 트리에서 특정 구간의 구간합을 구하는 과정을 쿼리라고 합니다. 2번~5번의 구간합을 구하는 과정을 예제로 살펴보겠습니다.
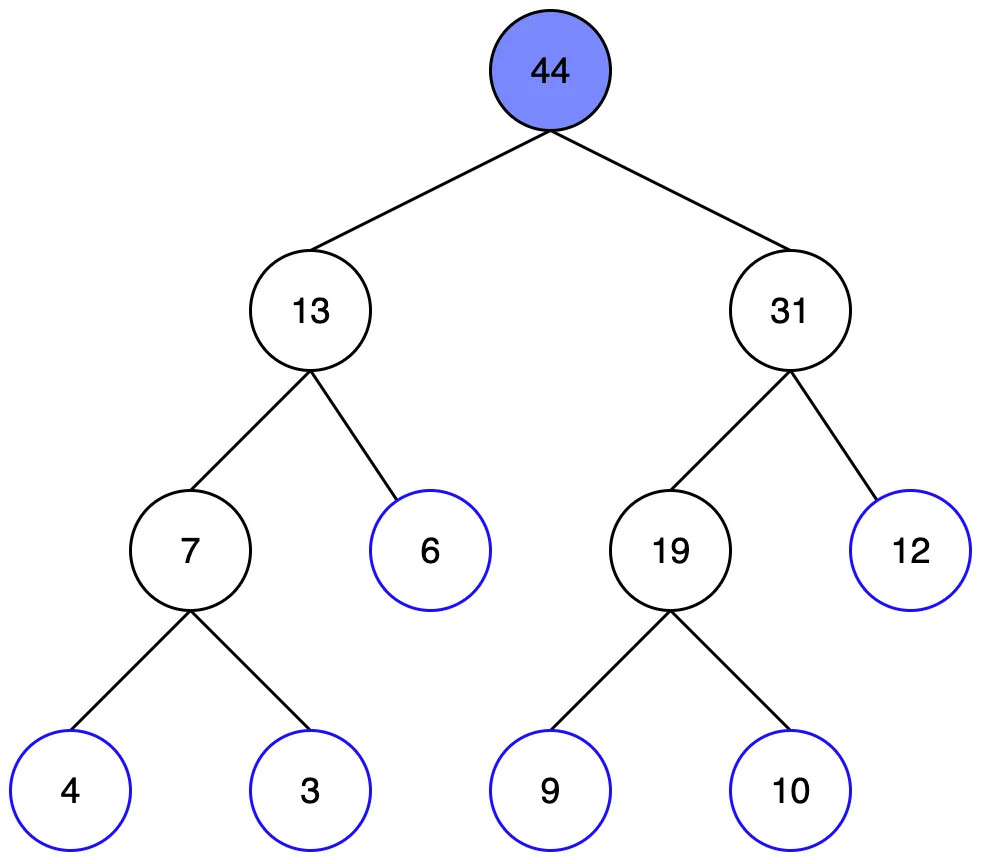
먼저 루트노드부터 탐색합니다. 찾는 범위보다 더 많은 구간을 포함하고 있으므로 자식 노드를 살펴봐야 합니다.
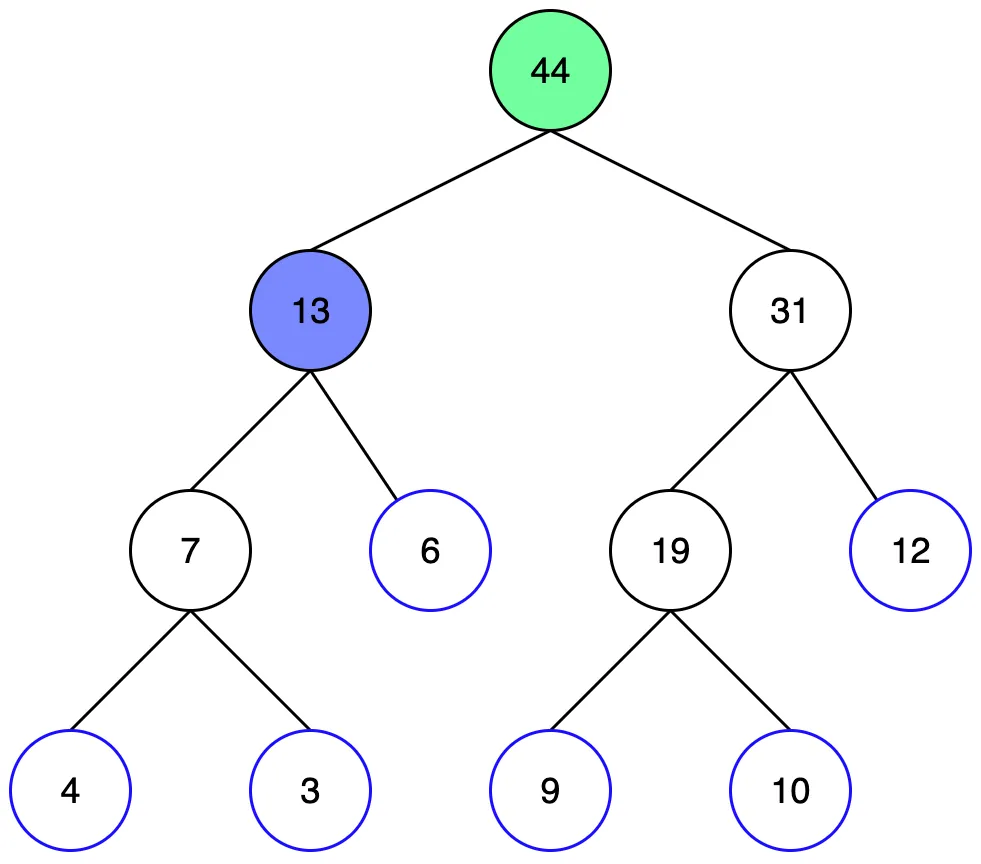
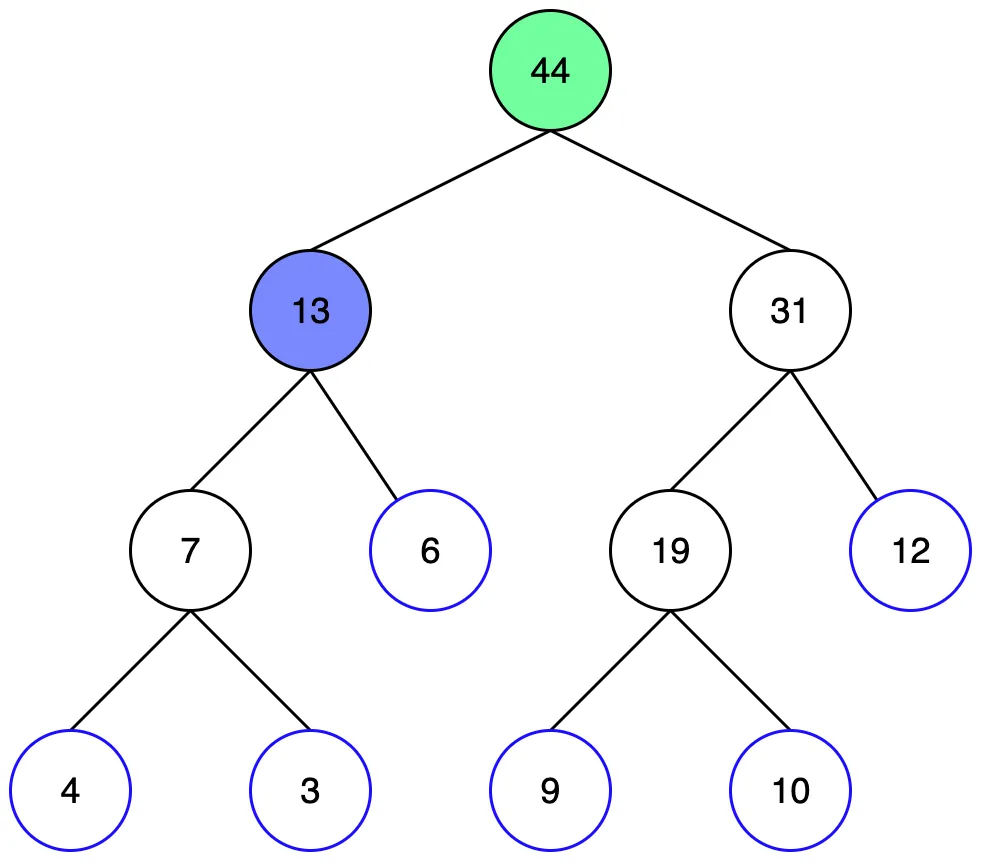
자식노드 역시 범위보다 더 많은 구간을 포함하고 있어서 자식노드를 살펴봐야 합니다. 완전히 범위에 포함되는 노드가 나올때까지 반복합니다.
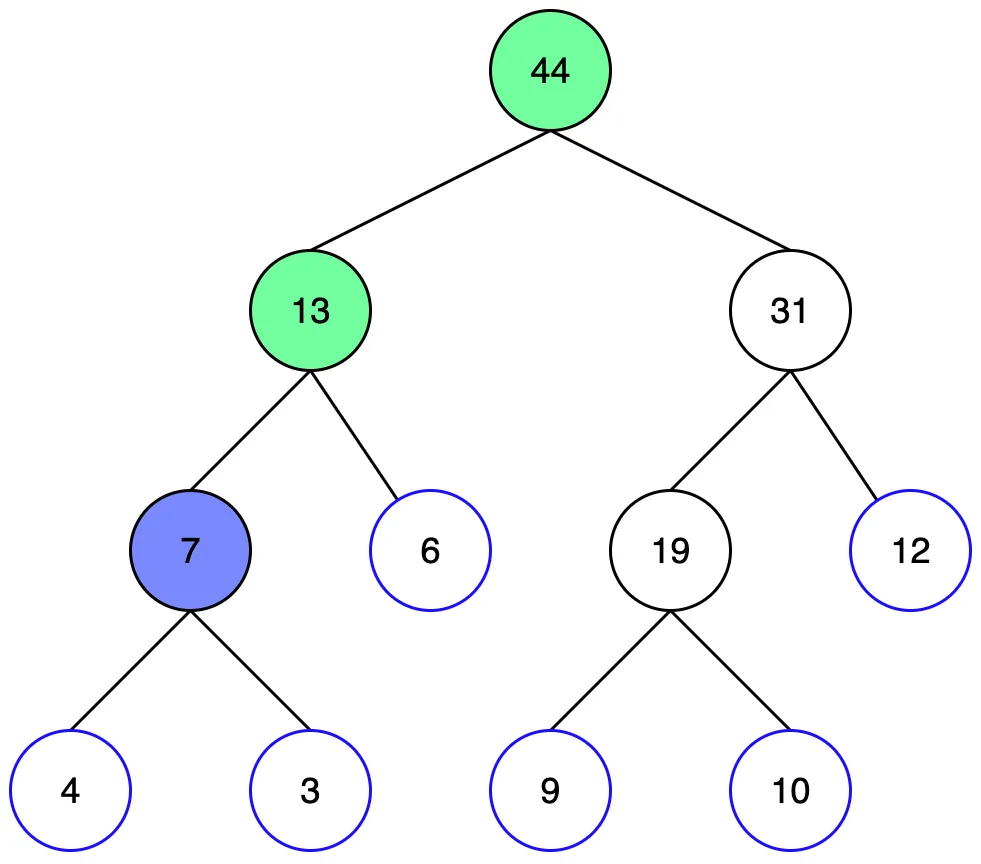
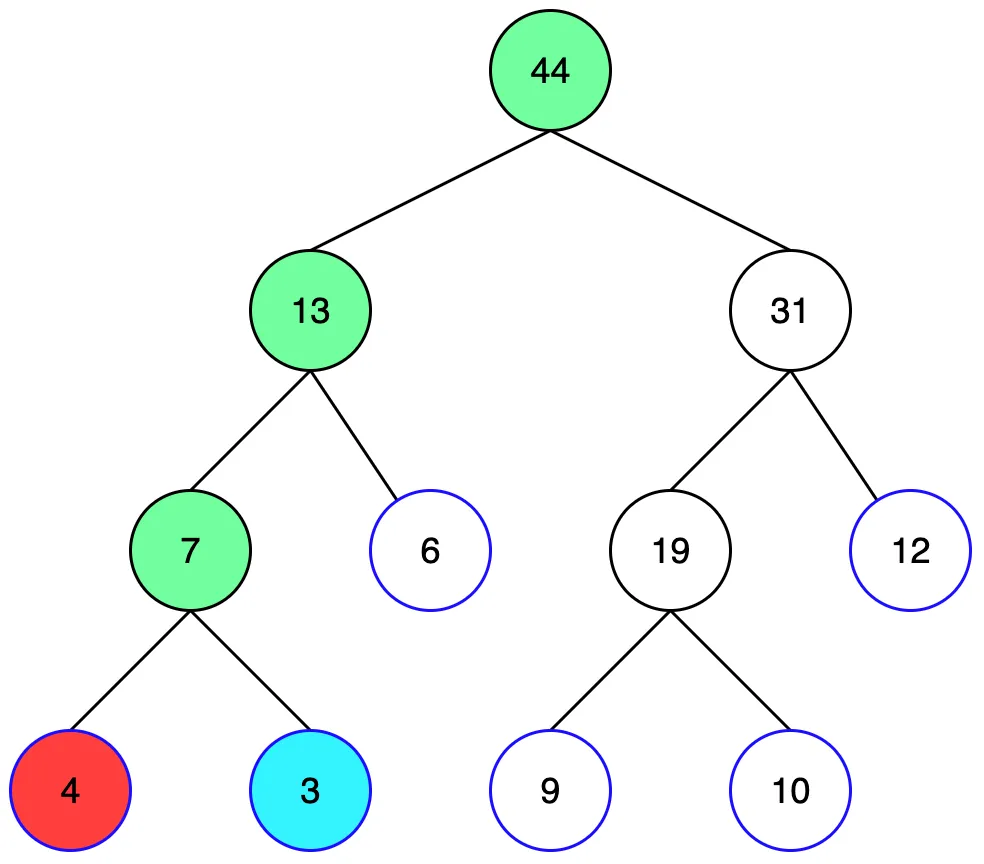
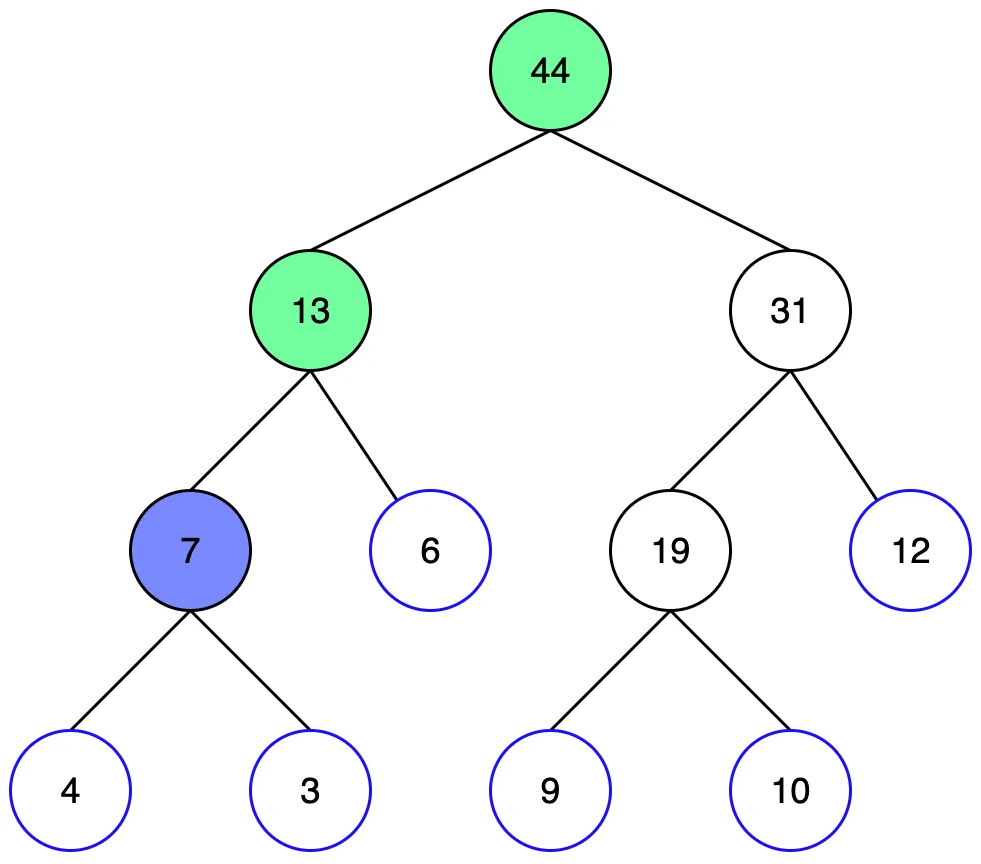
반복하다보니 리프노드까지 왔습니다. 하지만 1번 리프노드는 범위에 포함되지 않기때문에 형제 노드를 살펴봐야 합니다.
2번 리프노드는 구하려는 범위에 포함됩니다. 3을 정답값에 더합니다.
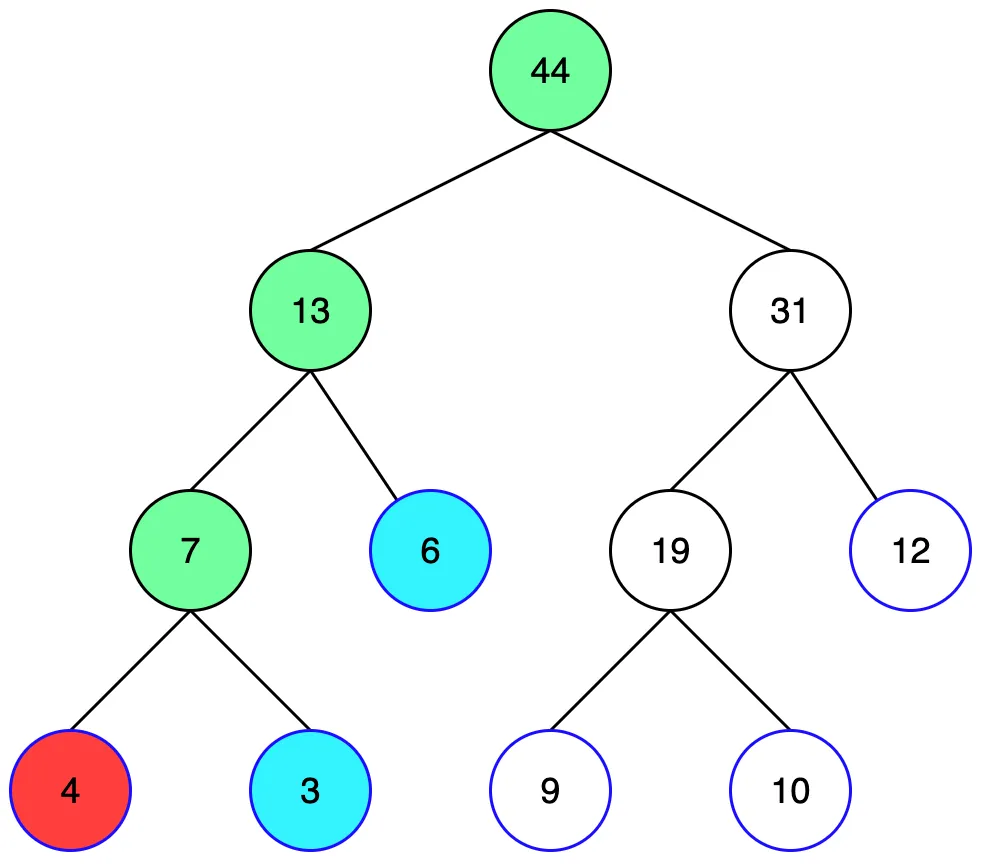
3번 리프노드 역시 구간에 포함되기 때문에 정답값에 6을 더해 9를 저장합니다.
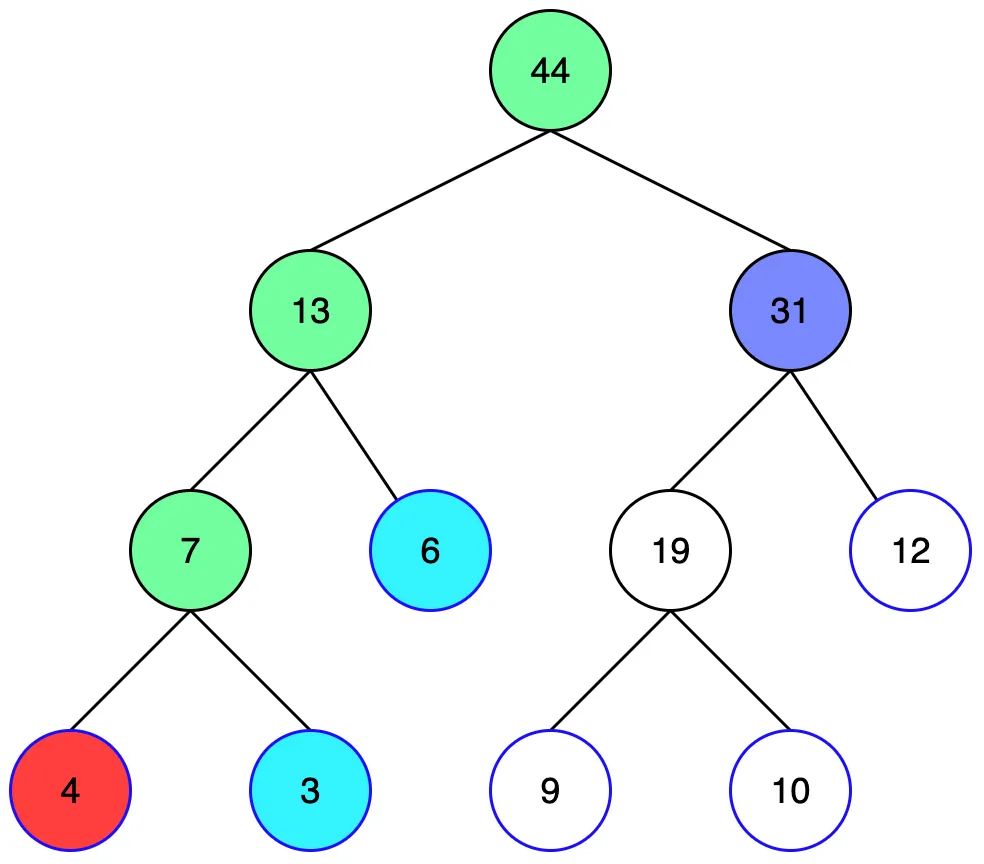
루트노드의 왼쪽 자식 노드를 모두 검사했으므로 오른쪽 자식노드를 탐색합니다. 해당 노드는 구하려는 범위를 초과하므로 자식 노드를 검사해야 합니다.
왼쪽 자식 노드는 2~5 구간중 4~5 구간합을 저장하고 있습니다. 해당 노드의 자식 노드를 검사하지 않아도 되기때문에 바로 정답값에 19를 더합니다. 최종적으로 2~5번 구간합은 28 이라는 답을 구할 수 있습니다.
쿼리를 코드로 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
# start, end: 구하고자 하는 범위 시작/끝
# left, right: 현재 탐색중인 노드의 범위
def query(node, start, end, left, right):
if right < start or end < left:
return 0
if start <= left and right <= end:
return tree[node]
mid = (left + right) // 2
return query(node * 2, start, end, left, mid) + \
query(node * 2 + 1, start, end, mid + 1, right)
업데이트
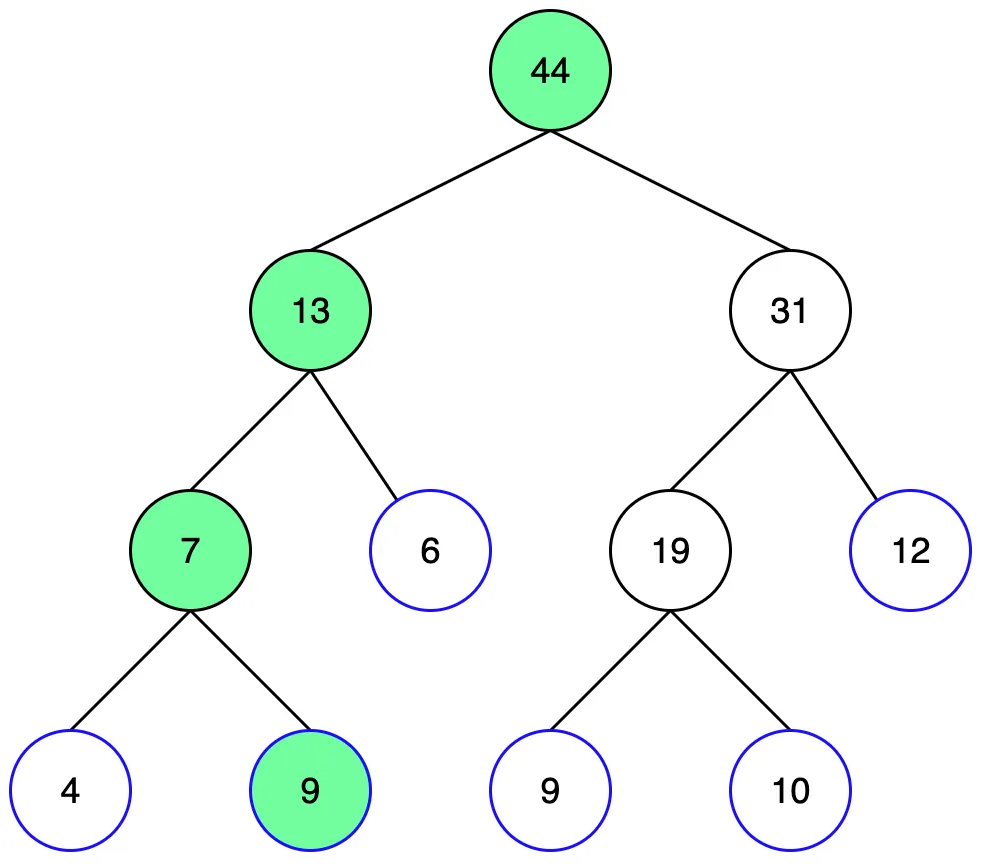
리프 노드의 값을 업데이트 하는 과정입니다. 2번에 6을 더하는 과정을 예제를 통해 살펴보겠습니다.
루트 노드부터 탐색합니다. 2번은 루트 노드의 왼쪽애 있으므로 왼쪽 자식을 탐색합니다.
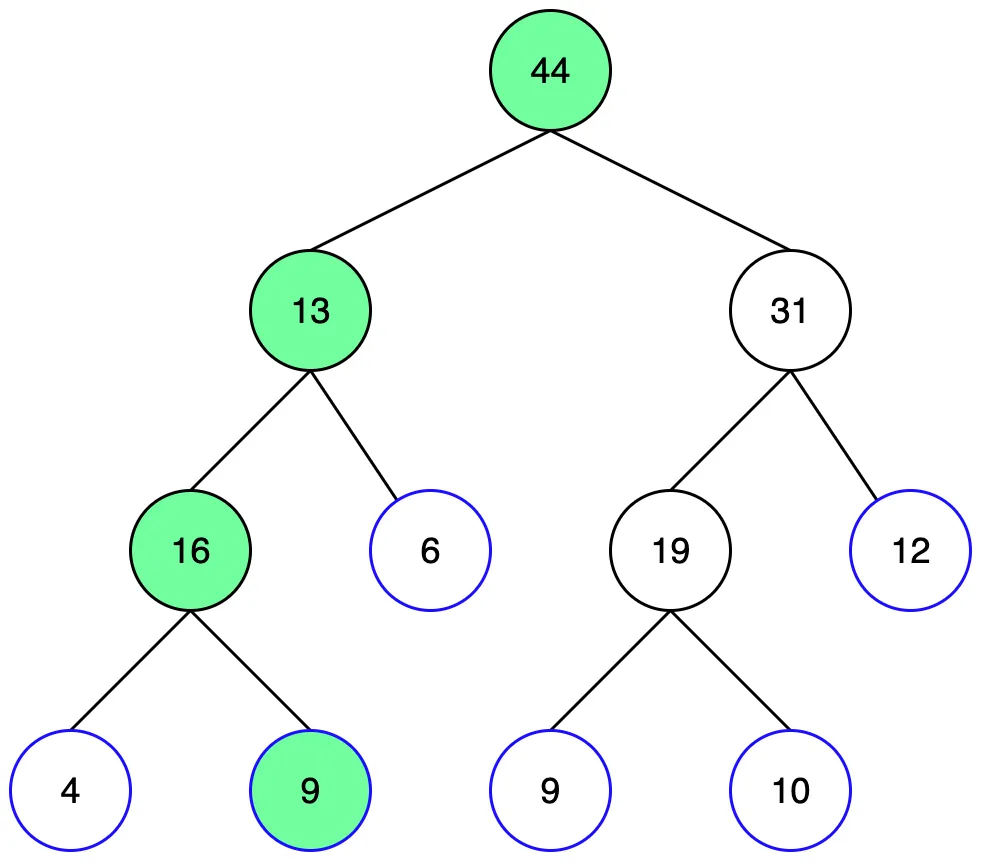
2번은 현 노드의 왼쪽에 있으므로 왼쪽 자식을 탐색합니다. 이렇게 원하는 리프노드에 도달할때까지 탐색을 반복합니다.
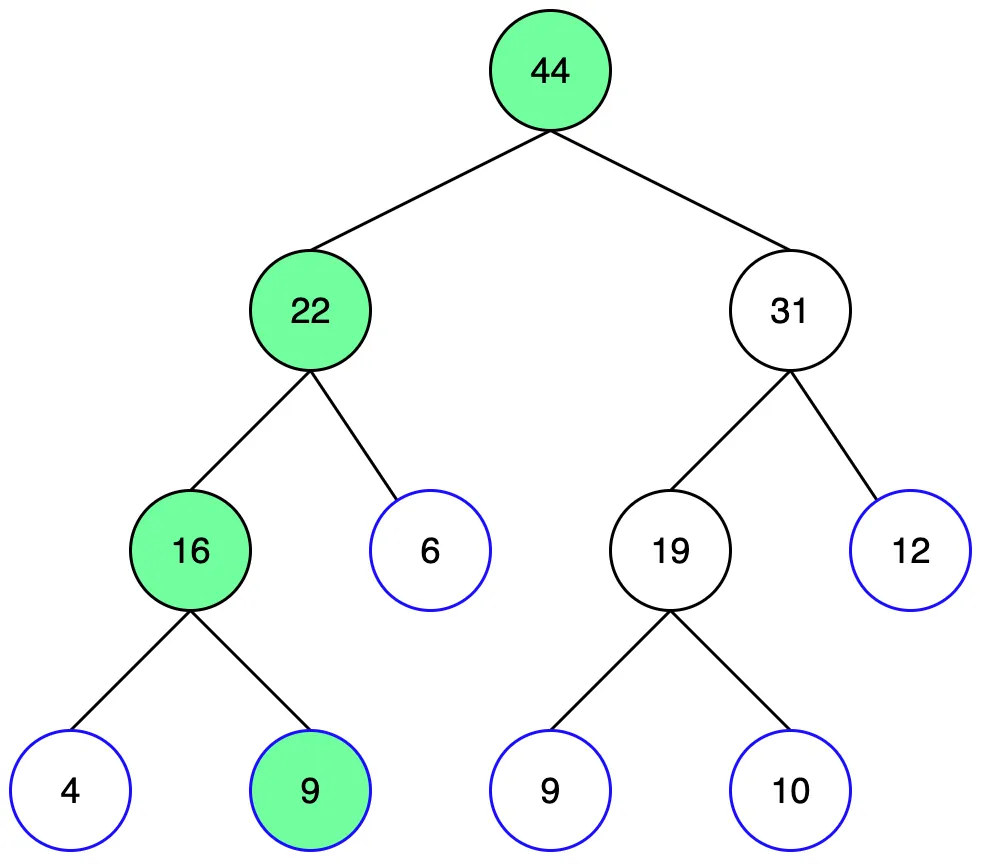
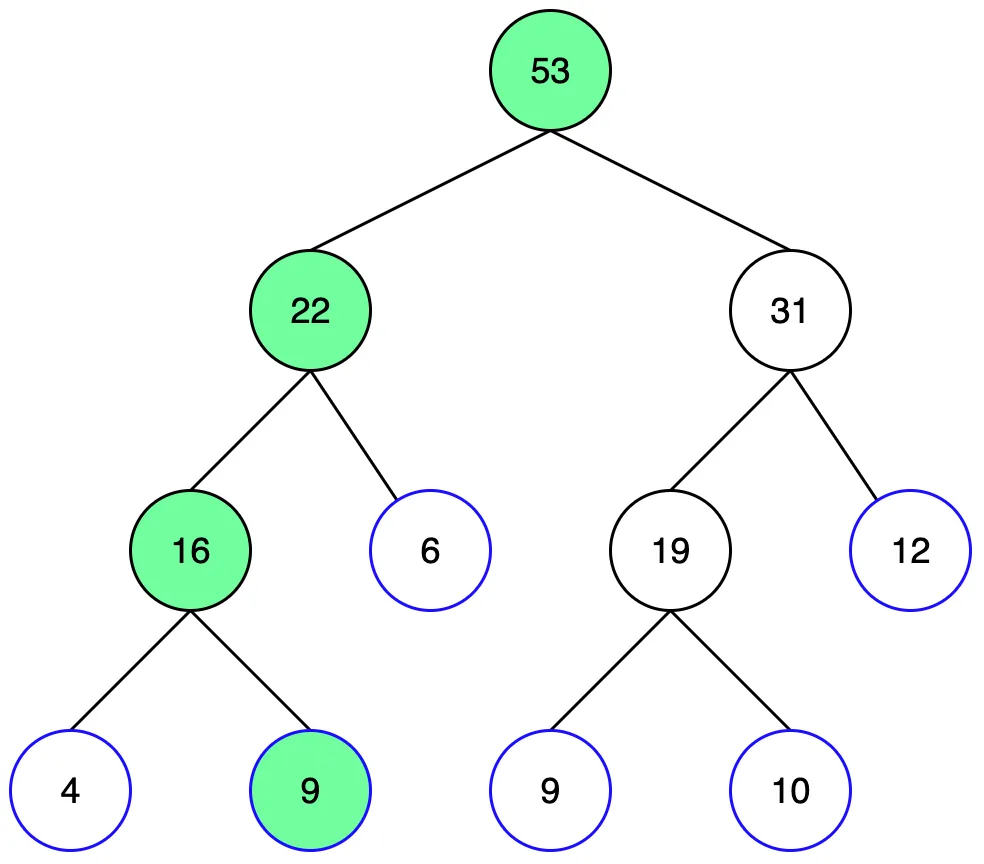
원하는 노드에 왔으니 6을 더해줍니다. 그 후 부모 노드들 역시 업데이트 해줍니다. 부모 노드까지 업데이트 끝나면 결과가 반영됩니다.
코드로 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
def update(node, left, right, idx, value):
if left == right:
tree[node] += value
return tree[node]
mid = (left + right) // 2
if idx < mid:
update(node * 2, left, mid, idx, value)
else:
update(node * 2 + 1, mid + 1, right, value)
tree[node] = tree[node * 2] + tree[node * 2 + 1]
세그먼트 트리는 백준에서 구간합의 범위가 넓을때 많이 사용됩니다. 하지만 여기서 더 나아가 여러 구간을 한번에 업데이트 하거나 더 많은 값을 업데이트 해야할때는 어떻게 해야할까요? 그 해답인 레이지 세그먼트를 다음에 알아보도록 하겠습니다.