개요
RNN과 LSTM은 요즘 핫한 문장 생성에 사용되는 transformer를 이해하는데 필요한 기초적인 신경망입니다. 문장, 음악과 같은 시퀀스 데이터 학습을 위한 신경망으로, 이전 데이터를 학습에 사용한다는 특징이 있습니다. 하나씩 자세히 알아보도록 하겠습니다.
RNN(Recurrent Neural Network)
출처: https://commons.wikimedia.org/wiki/File:Recurrent_neural_network_unfold.svg
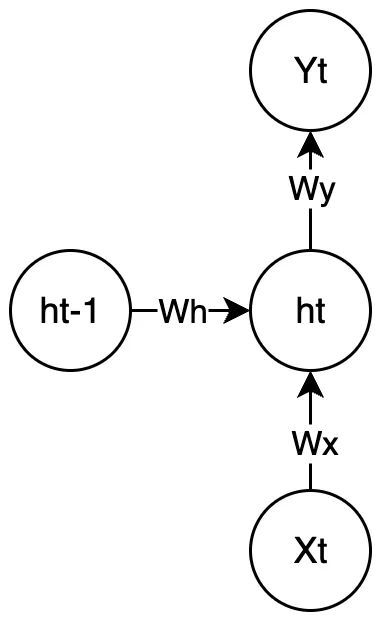
RNN은 이름에서 알 수 있듯이 순환 신경망입니다. 입력을 시간축으로 나누어 각 시점의 입력과 이전 hidden state를 함께 고려해서 새로운 hidden state를 계산합니다. 이전 hidden state를 사용하기 때문에 현재 입력된 시점의 이전 데이터도 활용이 가능합니다.
수식
RNN을 수식으로 보면 다음과 같습니다.
- \(x_t\): 현재 시점의 입력
- \(h_{t-1}\): 이전 시점의 hidden state
- \(h_t\): 새로운 hidden state
- \(f\): 활성화 함수(ReLU, Tanh 등)
- \(W_h, W_x\): 가중치
- \(b\): 바이어스
출력은 보통 \(y_t = W_y h_t\)로 계산됩니다.
RNN 종류
RNN은 신경망 구성에 따라 다양한 타입이 있습니다.
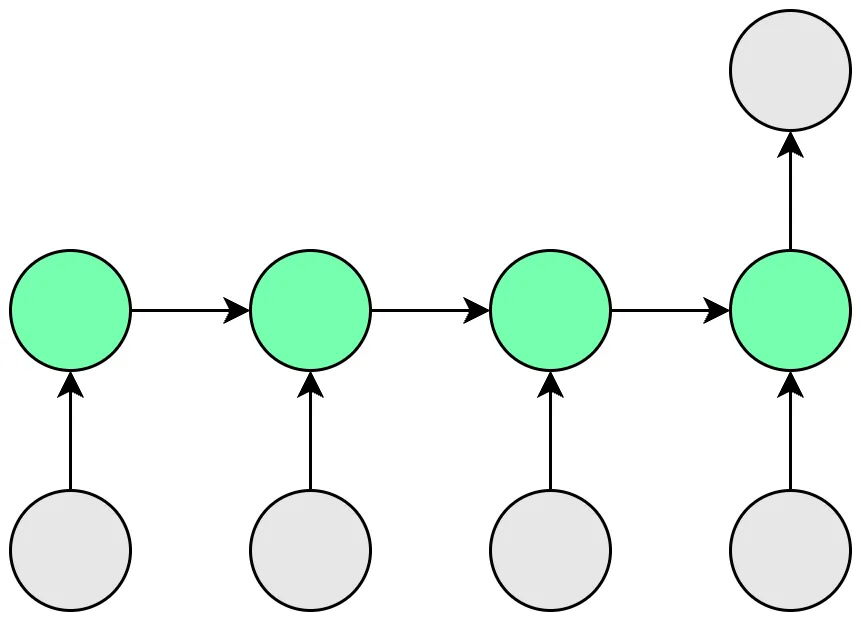
다대일(Many to One)
여러 입력을 통해 하나의 결과를 내는 타입입니다. 문장 분류와 같은 테스크에 사용됩니다.
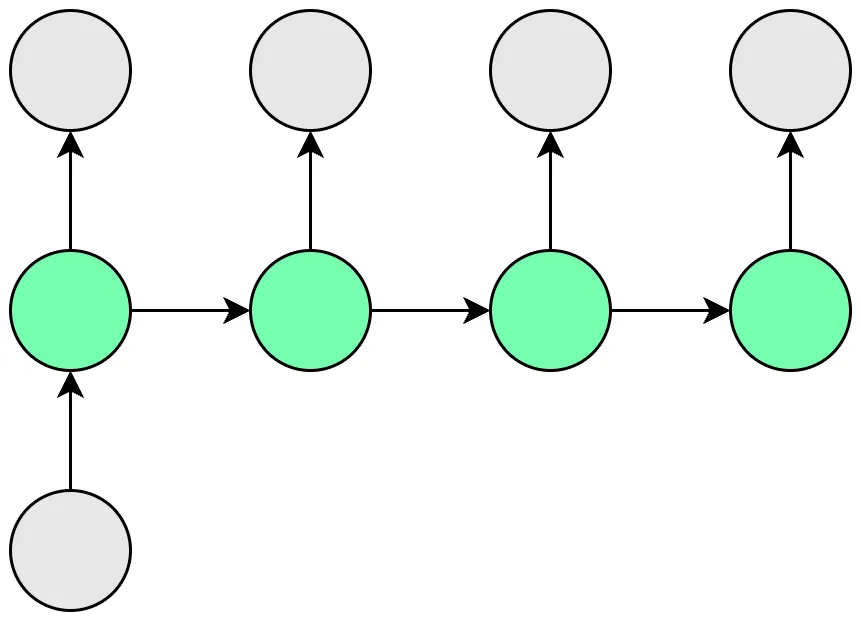
일대다(One to Many)
하나의 입력을 통해 여러 결과를 내는 타입입니다. 사진을 보고 설명하는 문장을 생성하는것과 같은 테스크에 사용됩니다.
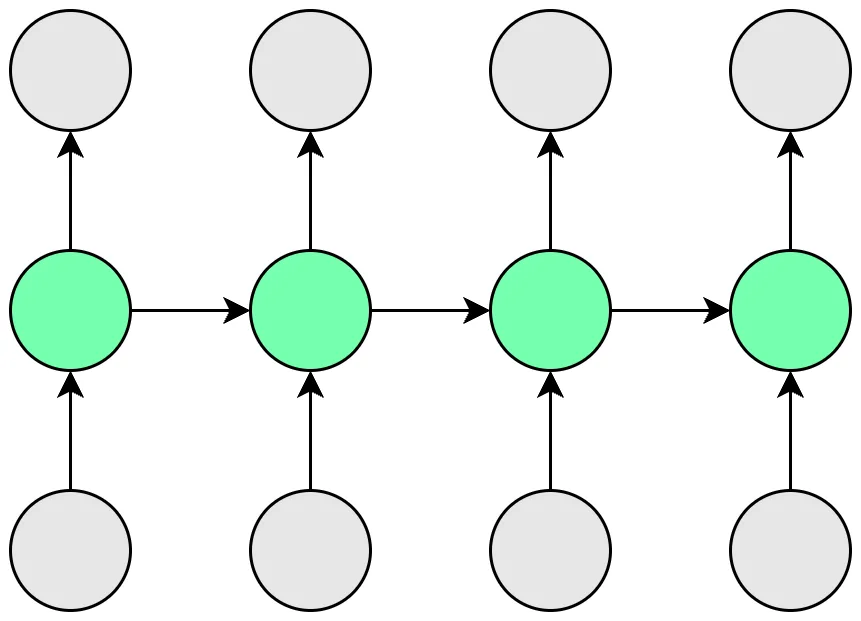
다대다(Many to Many)
여러 입력을 통해 여러 결과를 내는 타입입니다. 번역과 같은 테스크에 사용됩니다.
단점
RNN은 구조적으로 단점이 있습니다. 구조를 보면 hidden state가 시간이 지날수록 누적되어 가는 형태임을 알 수 있습니다. 이렇게 누적되다보면 먼 시점의 정보가 점점 희미해져 잘 전달이 되지 않는 문제가 생깁니다. (Gradient Vanishing/Exploding) 이를 장기기억 문제라고 합니다. 그래서 이 문제를 해결하기 위해 LSTM이 고안됩니다.
LSTM (Long Short Terem Memory)
이름에서 알 수 있듯이 RNN의 장기기억 문제를 해결하기 위해 고안되었습니다. 여러 구조적인 개선을 통해 문제 해결을 시도했습니다.
구조
출처: https://www.researchgate.net/figure/Traditional-LSTM-model_fig1_387629868
구조를 보면 RNN과 다르게 상당히 복잡해진것을 확인할 수 있습니다. LSTM은 데이터를 큰 변화 없이 흘려보내는 cell state를 추가하여 데이터가 상대적으로 장기간 기억되게 만들었습니다. 각 셀은 이전 셀에서 hidden state와 cell state를 받아 현재 시점의 데이터를 forget gate, input gate, output gate라는 세개의 게이트를 거쳐 출력값과 state 업데이트를 진행합니다. 각 게이트와 업데이트 수식에 대해 상세히 알아보겠습니다.
Forget Gate
이전 셀 state에서 어떤 정보를 버릴지 결정합니다. 구한 값을 cell state에 곱해줍니다.
\[f_t = \sigma(W_f [h_{t-1}, x_t] + b_f)\]Input Gate
새로운 정보를 얼마나 추가할지 결정합니다. input gate는 시그모이드(그림상 왼쪽)와 tanh(그림상 오른쪽)를 거친 두 개의 출력을 곱하여 cell state에 더해줍니다.
\[i_t = \sigma(W_i [h_{t-1}, x_t] + b_i)\] \[g_t = \tanh(W_g [h{t-1}, x_t] + b_g)\]cell state 업데이트
forget/input gate에서 얻은 값들을 다음 식으로 조합해 cell state를 업데이트 합니다. 수식을 풀어서보면, 이전 데이터와 현재 입력된 데이터를 어느정도 비율로 기억하는지 계산한다고 설명할 수 있을것 같습니다.
\[C_t = f_t \cdot C_{t-1} + i_t \cdot g_t\]Output Gate
최종 hidden state를 산출합니다.
\[o_t = \sigma(W_o [h_{t-1}, x_t] + b_o)\] \[h_t = o_t \cdot \tanh(C_t)\]