레이지 세그먼트 트리는 세그먼트 트리에 대한 이해가 선행되어야 합니다. 아직 세그먼트 트리를 잘 모르신다면 [자료구조] 세그먼트 트리(Segmenmt Tree)를 먼저 읽고 오시는걸 추천합니다.
개요
세그먼트 트리는 구간합을 구하는데 시간복잡도를 줄여주는 좋은 자료구조 입니다.
하지만 구간을 정해 값을 업데이트하는 문제와 같이 더 복잡한 연산이 요구되는 문제를 풀때도 적용이 가능할까요?
i~j번째 수에 v를 더해야 한다고 할때, 기존 세그먼트 트리를 이용하면 수를 찾아 변경하는 연산을 j - i + 1번 해야합니다.
최악의 경우를 빅오 표기법으로 나타내면 \(O(N \cdot log N)\) 입니다.
단순히 순차적으로 값을 더하는 연산은 \(O(N)\) 이므로 오히려 단순 반복이 더 빠른 상황이 발생합니다.
그래서 고안된 방법이 레이지 세그먼트 트리 입니다.
레이지 세그먼트 트리?
레이지 세그먼트 트리는 이름 그대로 느리게 노드를 갱신하는 트리입니다. 특정 조건을 만족하면 자식 노드에 변경된 값을 즉시 반영하지 않고, 따로 저장해 두었다가 나중에 전파(propagate)합니다. 이렇게 하면 불필요한 업데이트를 줄여 효율적인 업데이트가 이루어 질 수 있습니다. 예제를 통해 자세히 살펴보겠습니다.
초기화
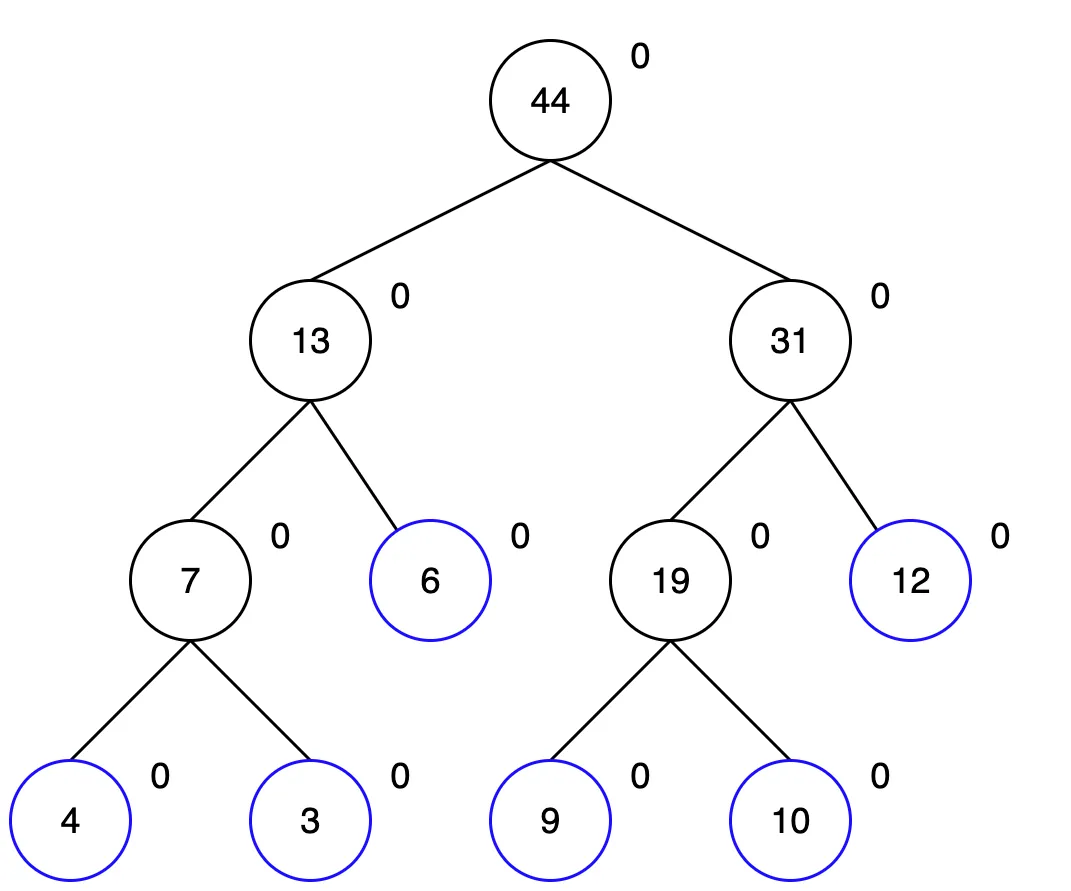
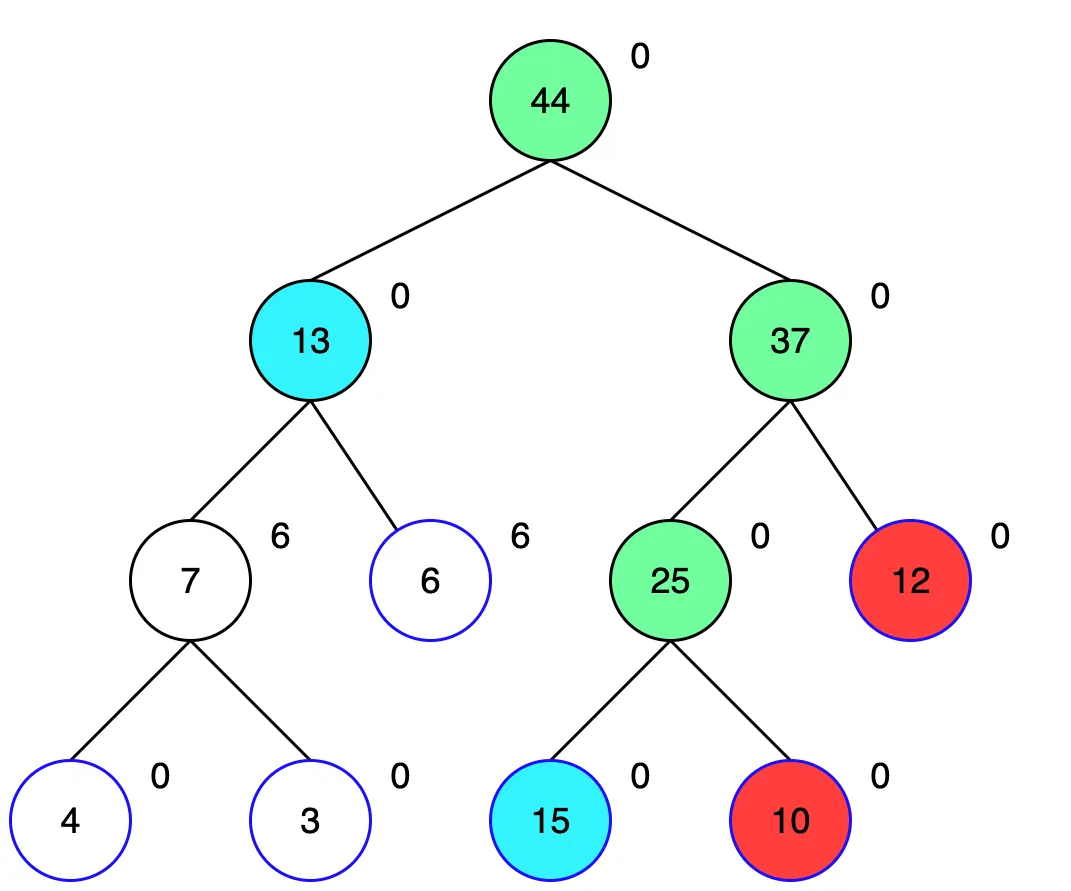
[4, 3, 6, 9, 10, 12] 6개의 숫자 리스트를 예제로 살펴보겠습니다.
세그먼트 트리와 구성이 거의 같지만, 각 노드 오른쪽 위에 숫자가 하나 추가된것을 볼 수 있습니다. 저게 바로 당장 업데이트가 필요 없을 경우 업데이트할 값을 저장해두기 위한 변수입니다.
초기화를 코드로 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
# node: [value, lazy]
tree = [[0, 0] for _ in range(4 * n)]
def init(node, left, right):
if left == right:
tree[node] = [data[left - 1], 0]
return
mid = (left + right) // 2
init(node * 2, left, mid)
init(node * 2 + 1, mid + 1, right)
tree[node] = [tree[node * 2][0] + tree[node * 2 + 1][0], 0]
구간 업데이트
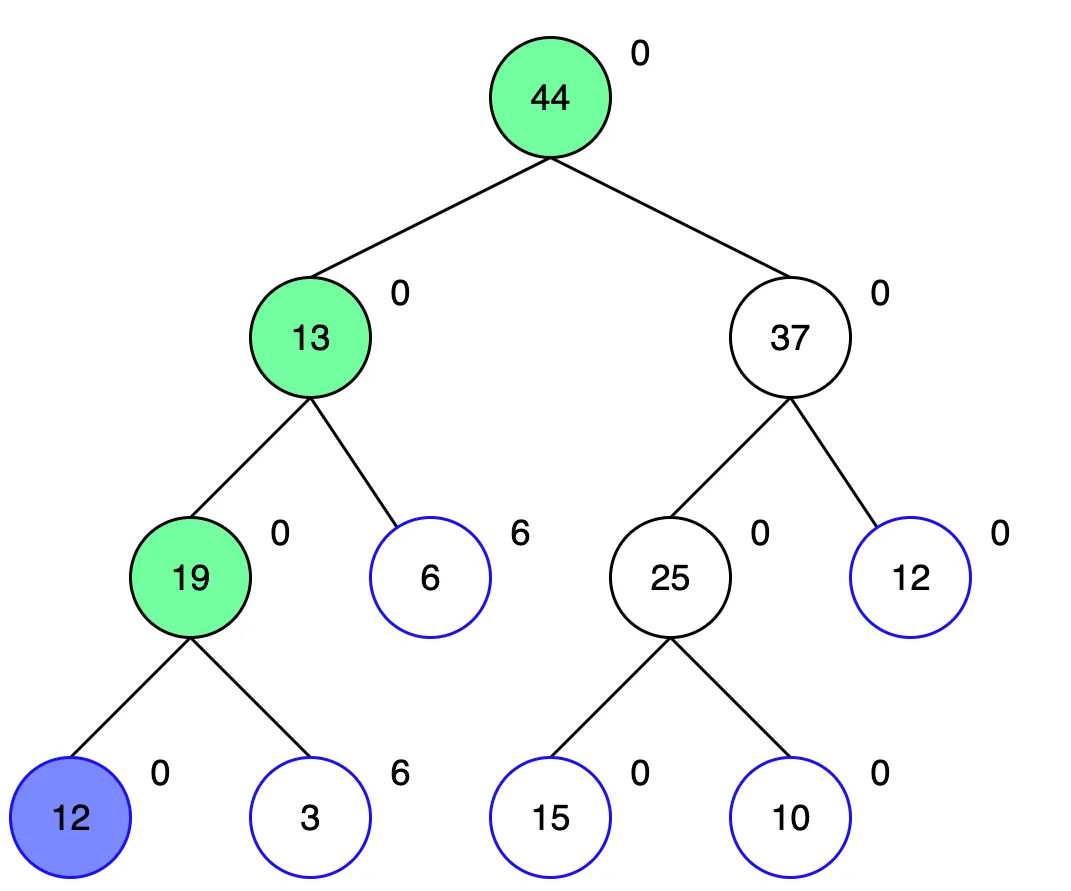
구간을 정해 구간의 값을 업데이트 하는 과정입니다. 1~4번에 6을 더하는 과정을 예제를 통해 살펴보겠습니다.
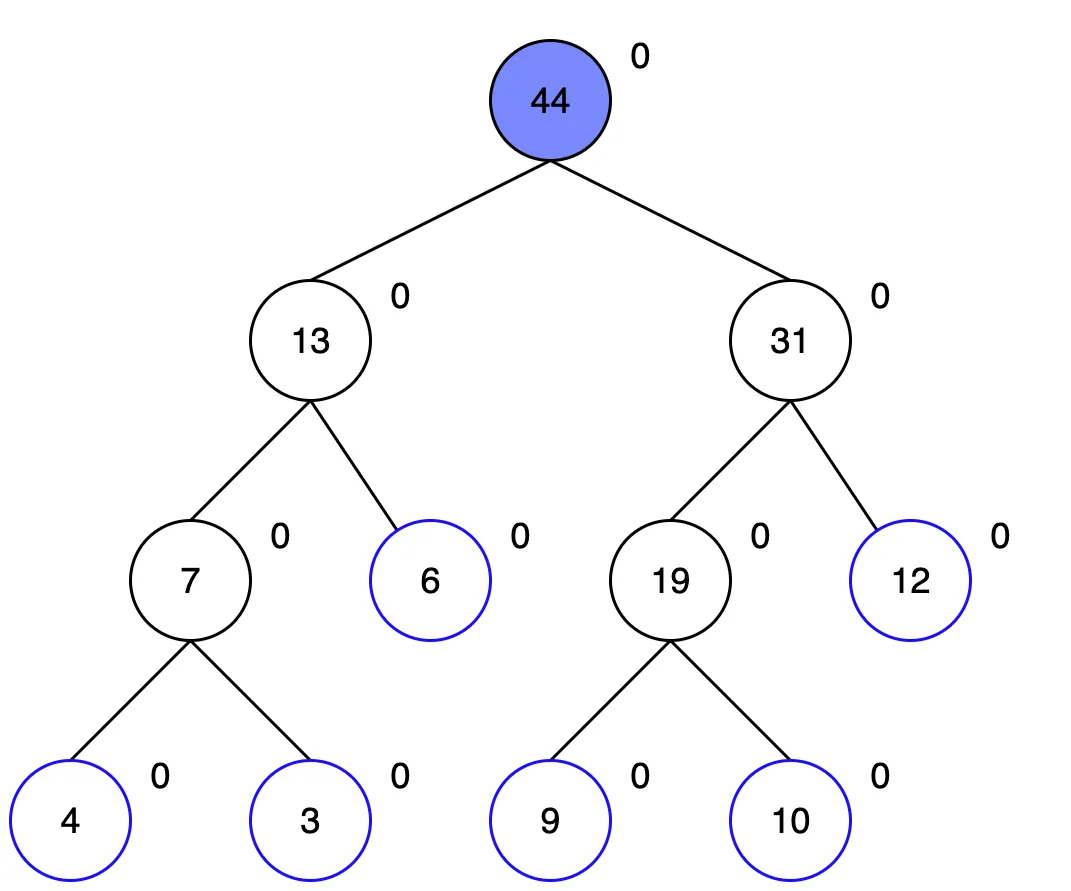
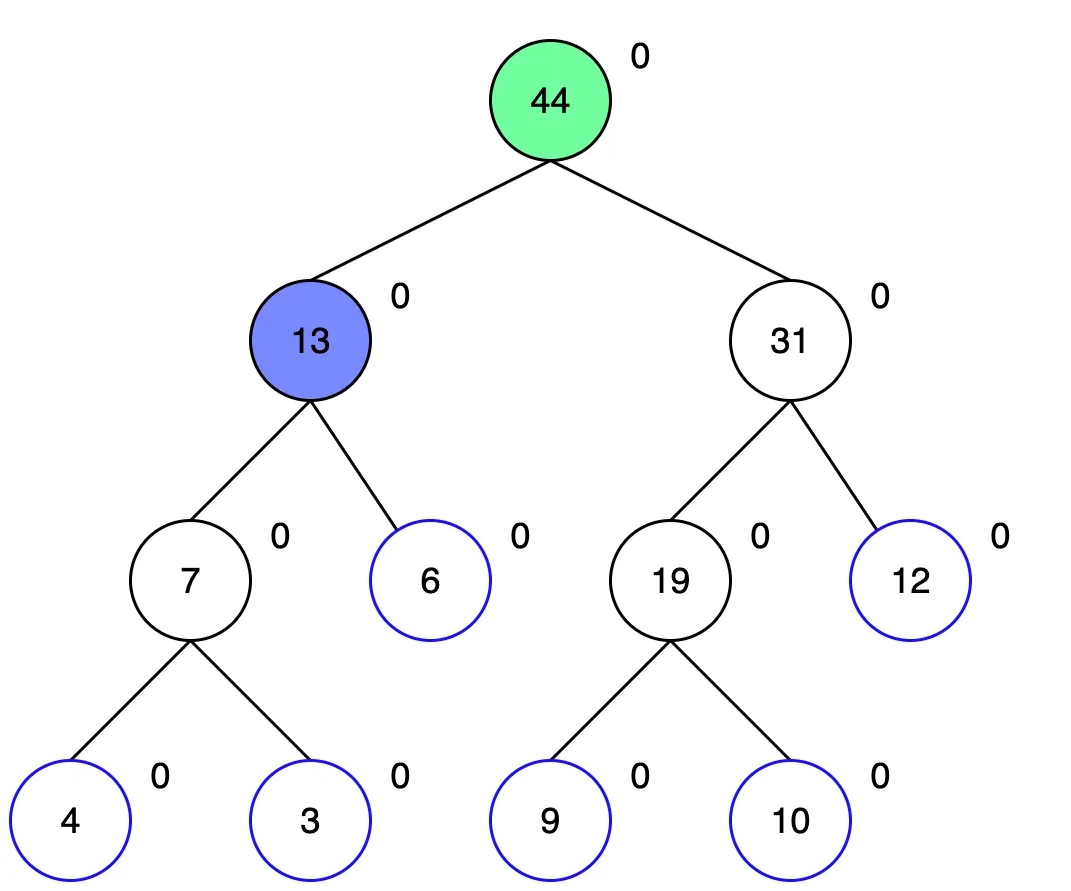
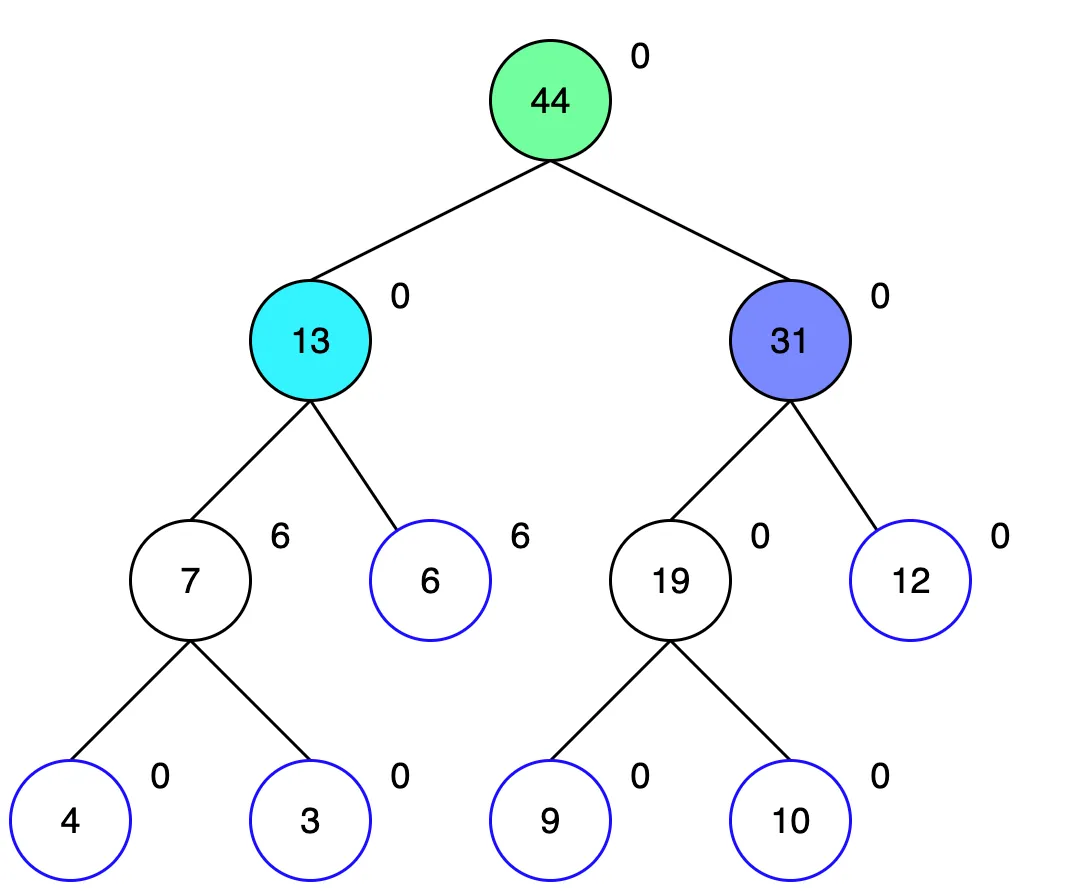
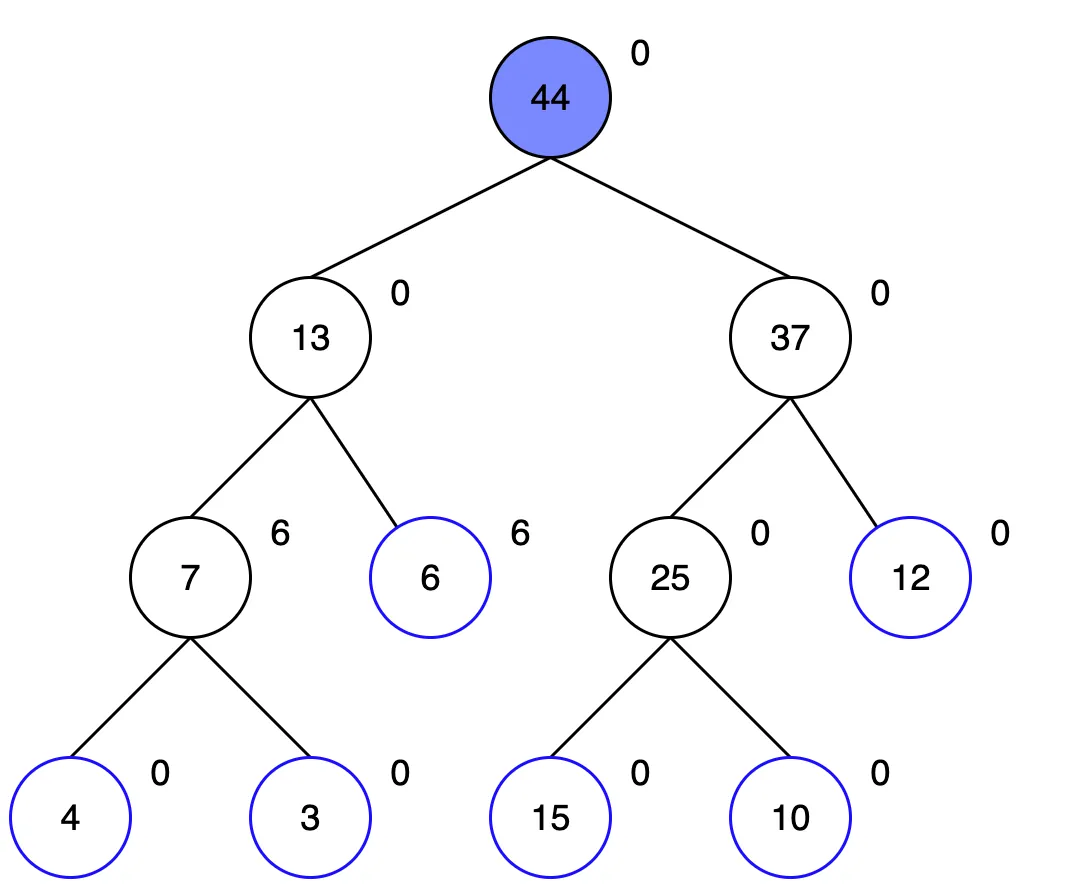
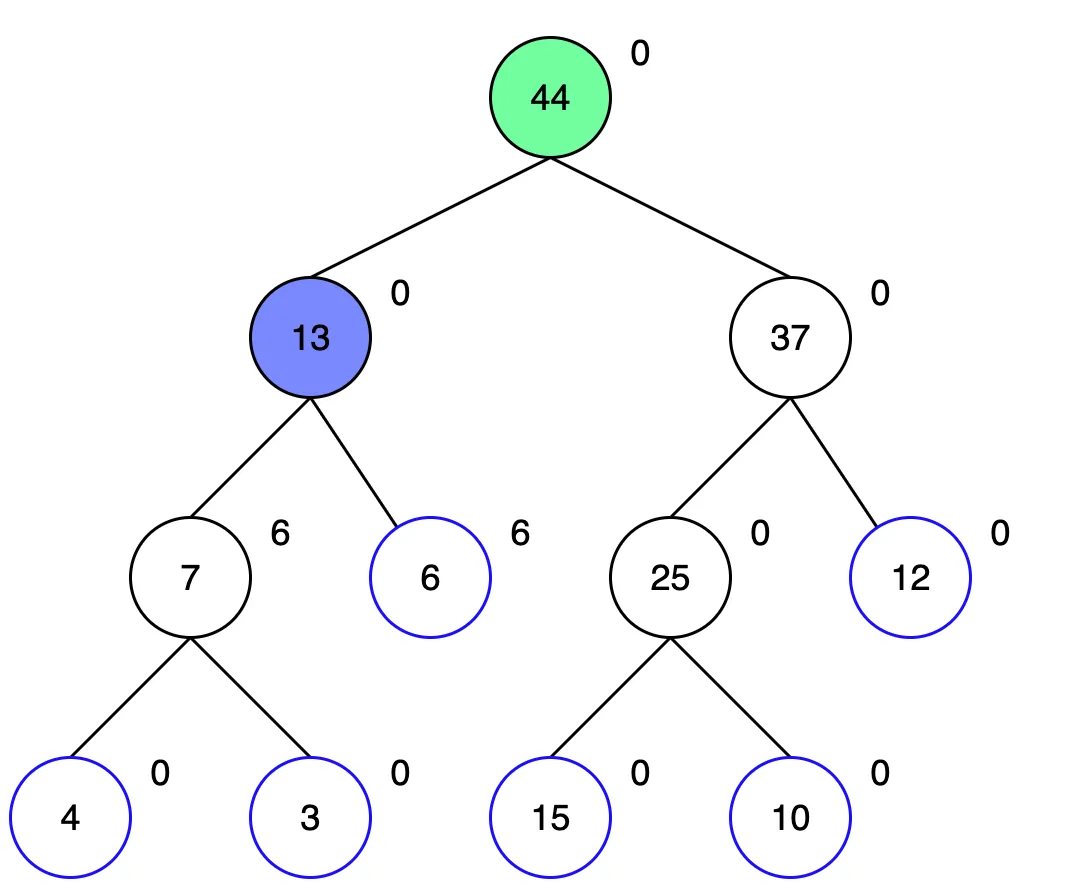
루트 노드부터 탐색합니다. 1~3번 구간에 해당하는 루트 노드의 왼쪽 자식노드 부터 탐색합니다.
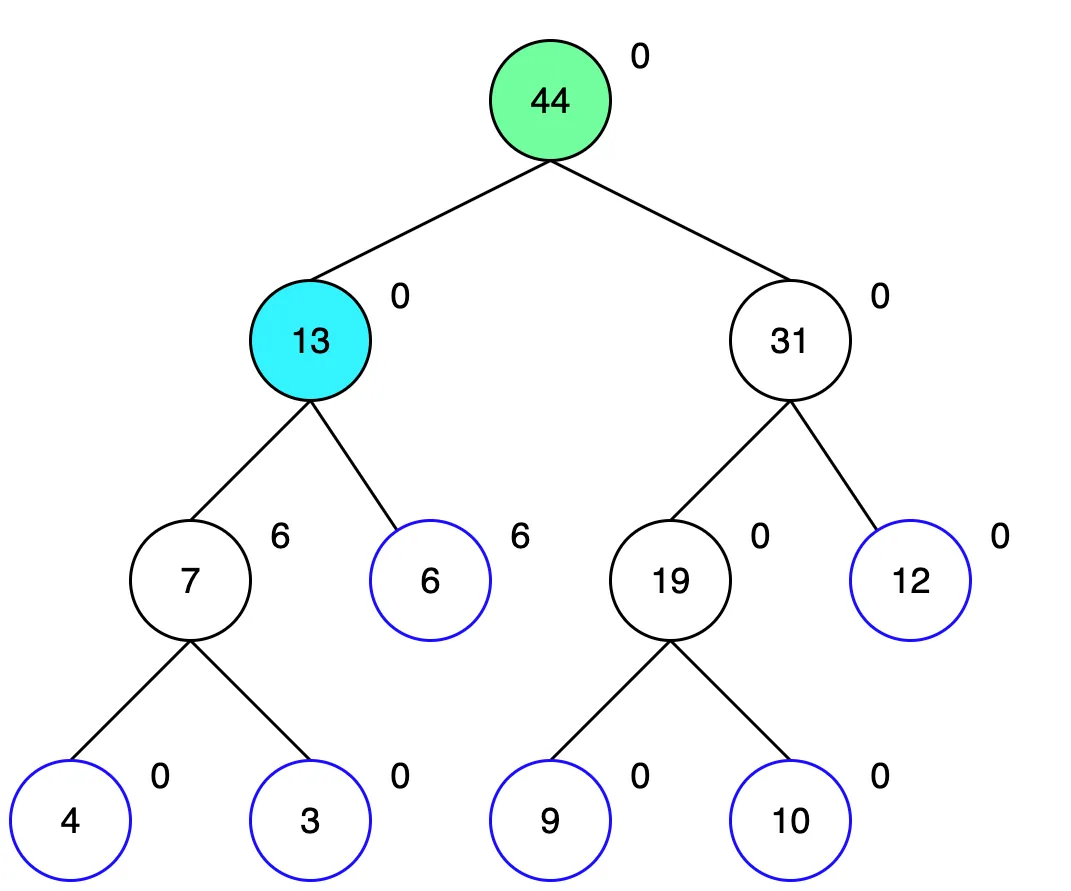
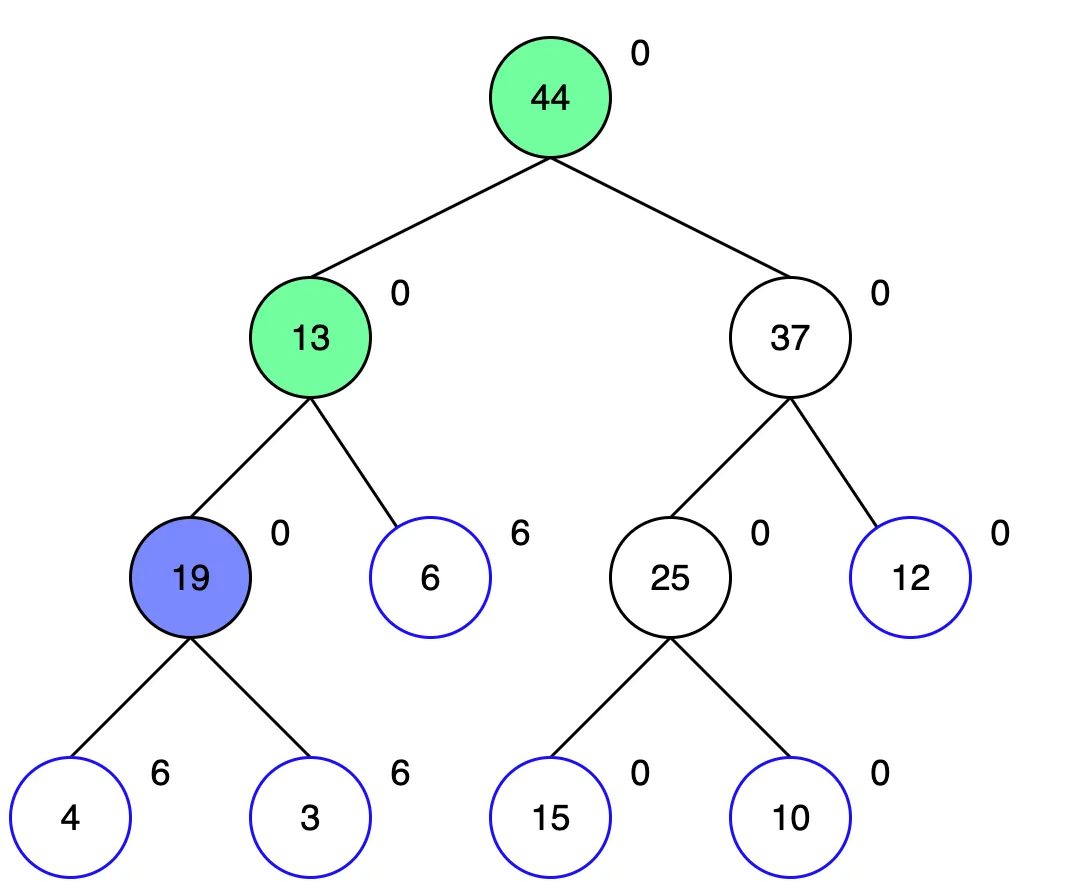
해당 노드의 왼쪽은 1~2번, 오른쪽은 3번을 포함합니다. 이 두 자식 모두 업데이트 범위에 포함되므로 더 내려가볼 필요가 없습니다. 더 탐색해도 어차피 모두 6을 더해야 하는 노드들이기 때문입니다. 그래서 현재 노드에 6을 더해 값을 업데이트 하고, 두 자식 노드는 lazy에 6을 기억해둡니다.
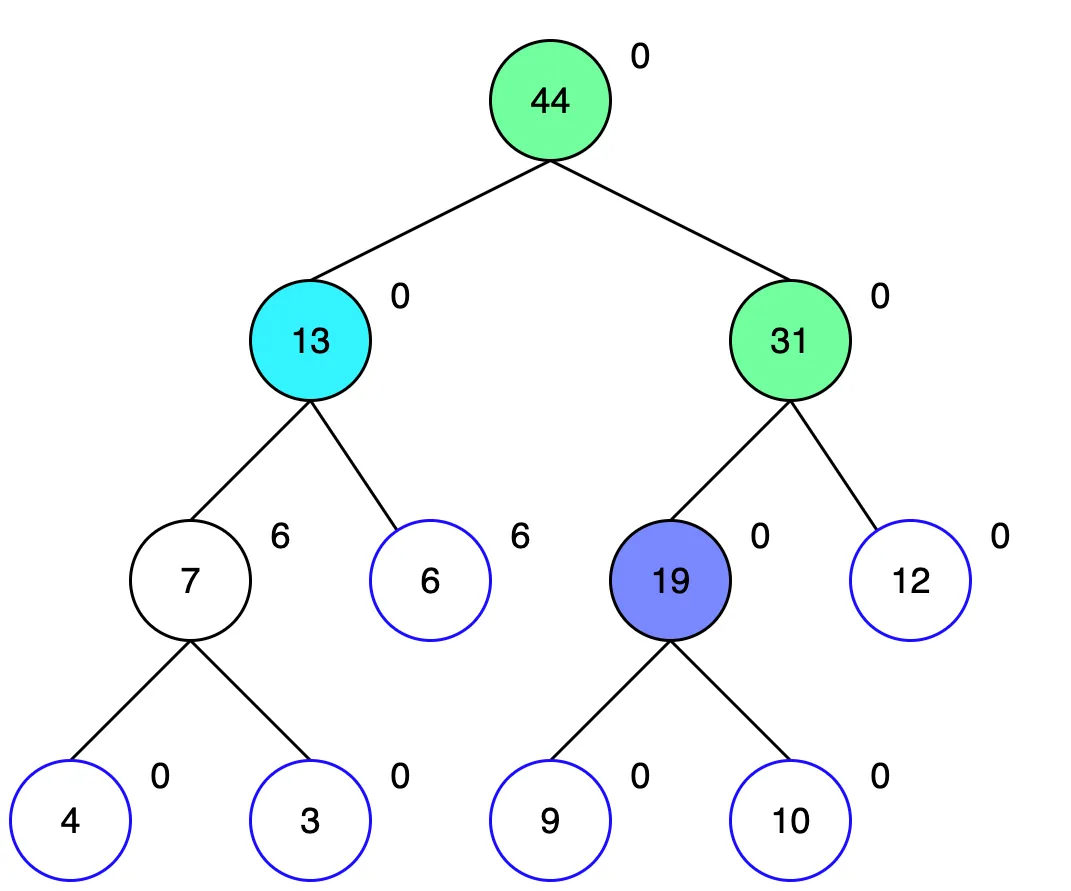
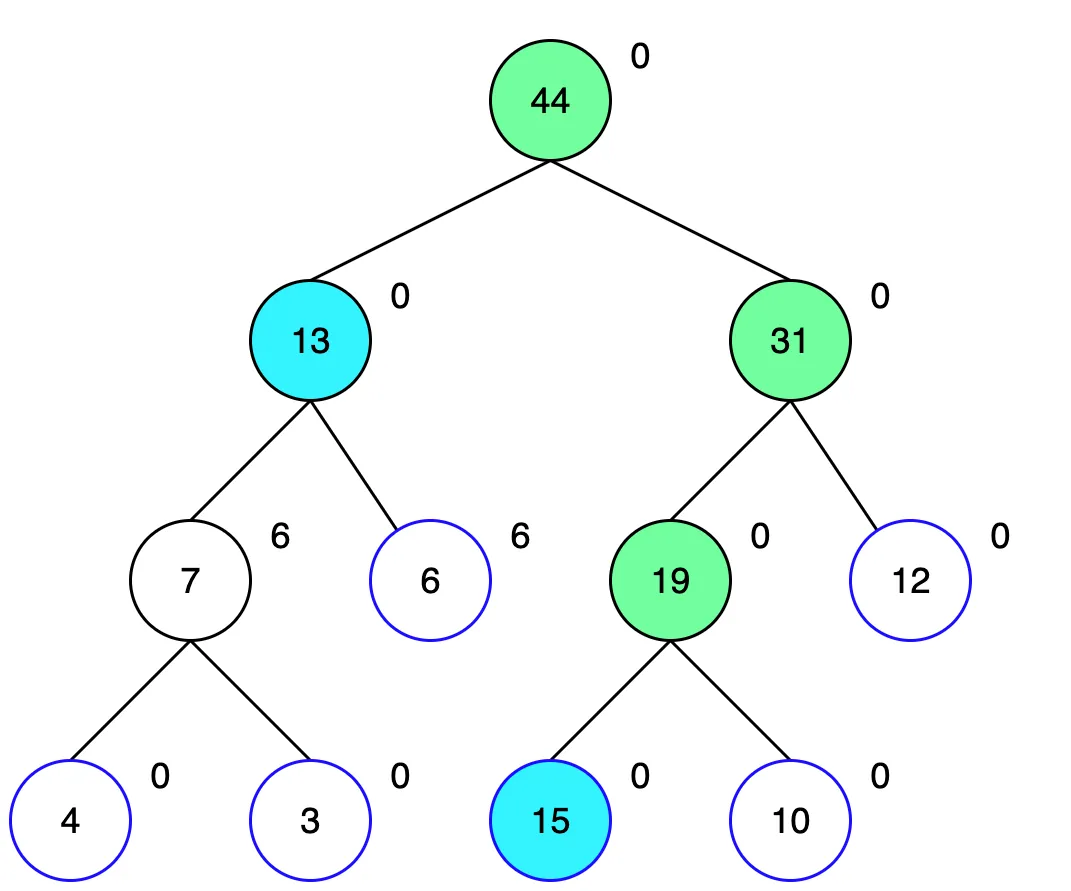
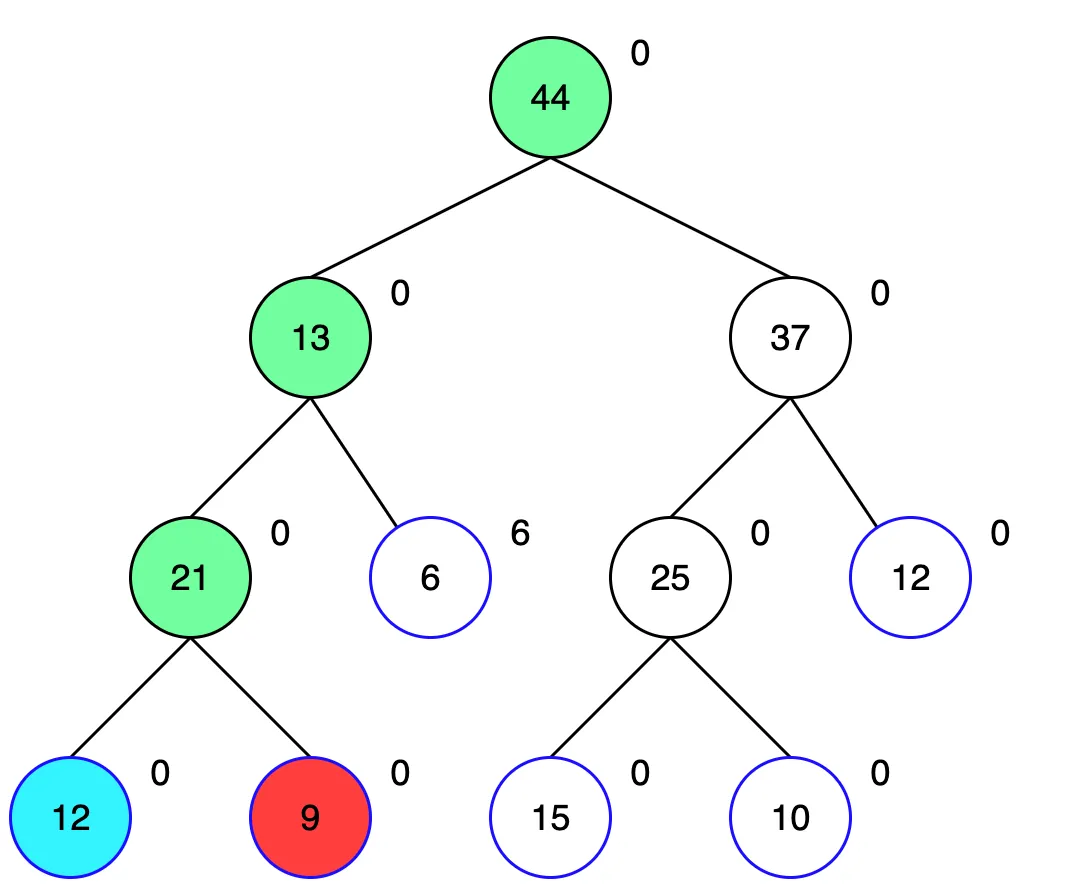
이제 루트 노드의 오른쪽 자식을 탐색합니다. 해당 노드는 4~6번을 포함하는 노드인데, 우리는 4번만 필요하므로 왼쪽 자식을 먼저 탐색합니다. 이런식으로 찾아 내려가다보면 리프노드까지 도달하게 되는데, 더 아래에는 업데이트할 노드가 없으므로 바로 6을 더해 15로 업데이트 해줍니다.
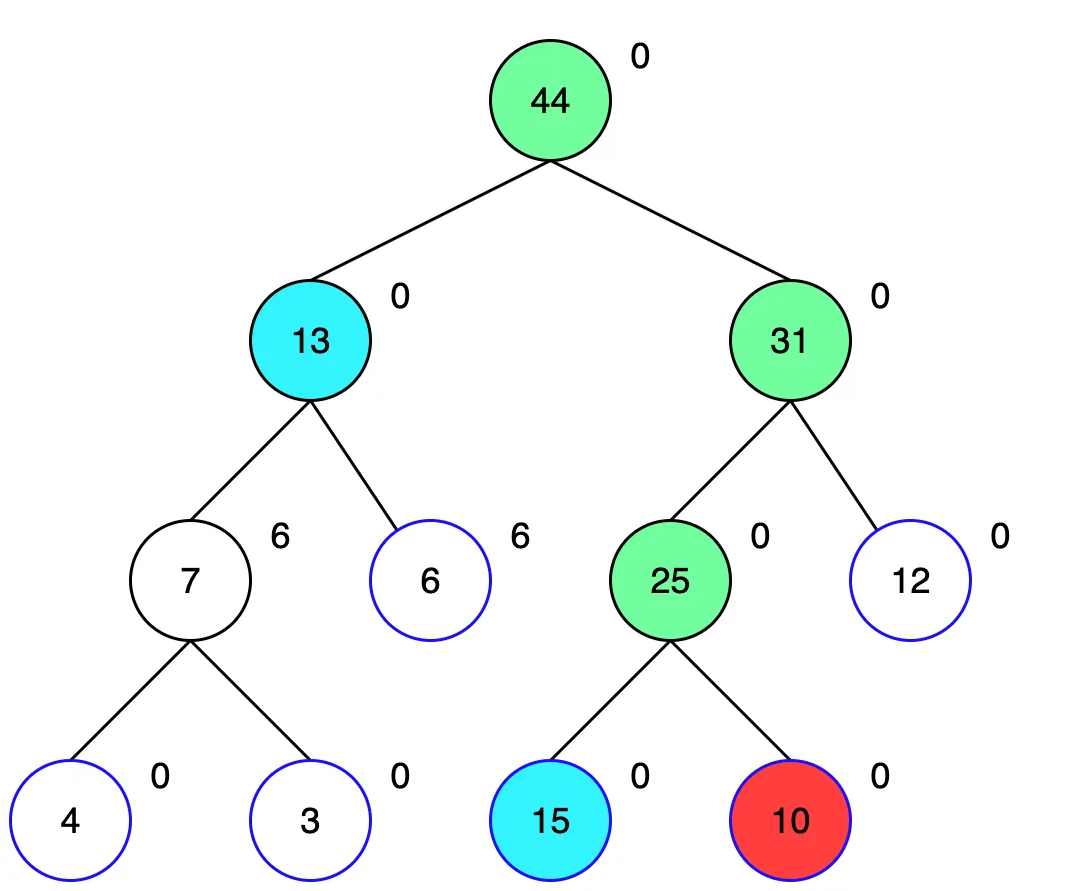
남은 두 자식은 범위에 포함되지 않으므로 부모 노드에도 6을 더해 값을 업데이트 해줍니다.
코드로 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
def update_range(node, start, end, left, right, value):
propagate(node, left, right)
if end < left or right < start:
return
if start <= left and right <= end:
tree[node][1] += value
propagate(node, left, right)
return
mid = (left + right) // 2
update_range(node * 2, start, end, left, mid, value)
update_range(node * 2 + 1, start, end, mid + 1, right, value)
tree[node][0] = tree[node * 2][0] + tree[node * 2 + 1][0]
예제 코드에서 propagate은 lazy에 저장된 데이터를 전파해야할 때 사용하는 함수입니다. 전파에 대한 내용은 바로 뒤에 설명하겠습니다.
전파(propagate)
전파는 lazy에 저장된 값을 실제 값으로 반영하는 과정입니다. 값을 업데이트 해야하는데 이미 lazy에 값이 있는 경우, 구간합을 찾는데 아직 lazy에 값이 있어 업데이트 되지 않는 경우 실행합니다. 구간 업데이트에서 구간합을 진행한 상태에서 1번 노드에 2를 더하는 상황을 예제로 알아보겠습니다.
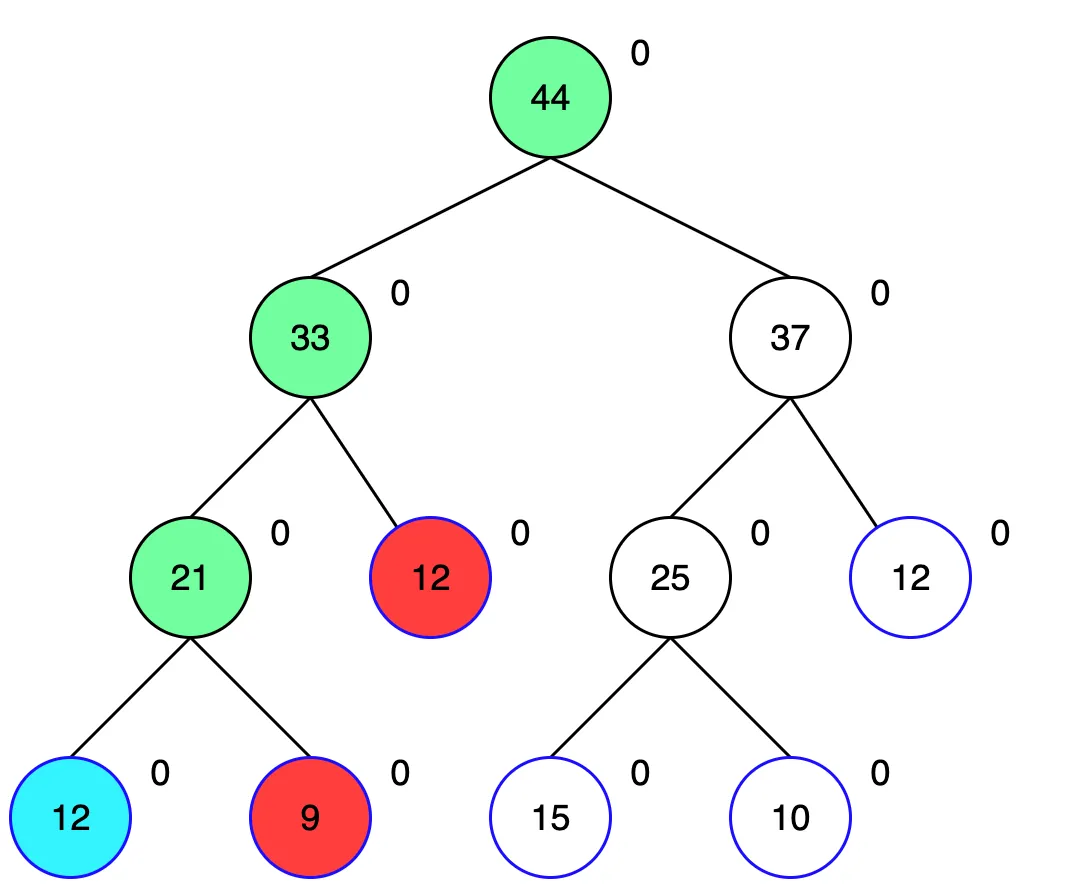
루트노드부터 시작해서 목표인 1번 값이 있는 노드까지 찾아 내려갑니다.
그런데 내려가다 보니 이전에 lazy에 값을 저장해두고 아직 업데이트 하지 않는 노드가 있습니다.
새로운 값을 반영하기 위해 lazy에 있는 값은 더해 업데이트 해주고 넘어가야 합니다.
이때 해당 노드는 1~2번 노드의 구간합을 담당하므로 (2-1+1) * lazy 값을 더해야 합니다.
lazy값은 모든 자식 노드에 더해지는 값이기 때문입니다.
일반화 하면 (right - left + 1) * lazy라고 표현할 수 있습니다.
lazy에 있던 값을 자식노드의 lazy에도 전달하여 업데이트 할 수 있도록 합니다.
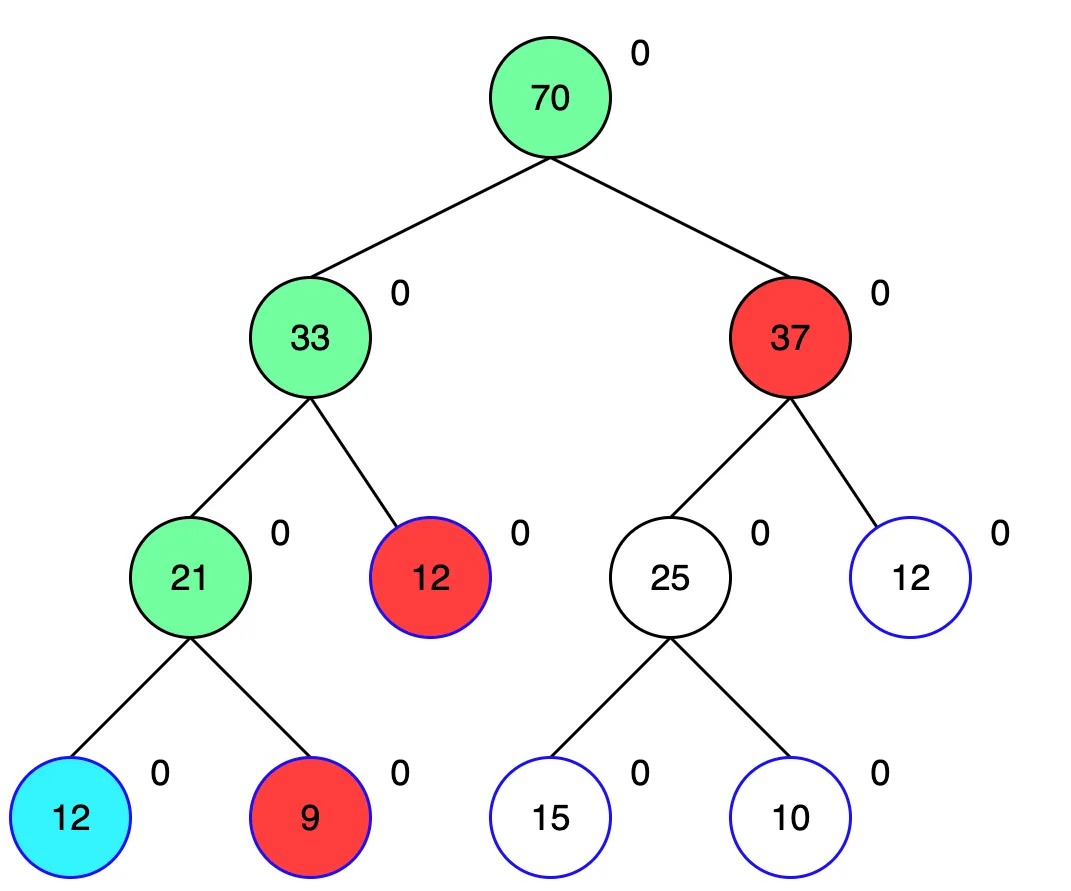
목표인 1번 리프노드에 도달했습니다. lazy에 있는 값과 목표인 2를 더해 업데이트 해줍니다.
이제 다른 나머지 자식 노드들을 보며 부모 노드의 구간합을 업데이트 해줍니다. 이 과정에서 아직 반영되지 않은 lazy값이 있으면 모두 반영해 줍니다.
코드로 구현하면 다음과 같습니다.
1
2
3
4
5
6
7
8
def propagate(node, left, right):
if tree[node][1] == 0:
return
tree[node][0] += (right - left + 1) * tree[node][1]
if left != right:
tree[node * 2][1] += tree[node][1]
tree[node * 2 + 1][1] += tree[node][1]
tree[node][1] = 0
쿼리
레이지 세그먼트 트리에서 특정 구간의 구간합을 구하는 과정은 세그먼트 트리에서 전파만 추가된 형태입니다. 그래서 따로 예제 그림으로 설명하지 않고 바로 코드로 구현하겠습니다.
1
2
3
4
5
6
7
8
9
def query(node, start, end, left, right):
propagate(node, left, right)
if right < start or end < left:
return 0
if start <= left and right <= end:
return tree[node][0]
mid = (left + right) // 2
return query(node * 2, start, end, left, mid) + \
query(node * 2 + 1, start, end, mid + 1, right)
세그먼트 트리의 쿼리 코드에서 맨 위에 propagate 호출만 추가되었습니다.
레이지 세그먼트 트리는 세그먼트 트리로 처리하기에 데이터 범위가 너무 넓을때 주로 사용합니다. 하지만 더욱 복잡한 문제를 해결해야 할때는 단순히 lazy propagation으로는 불가능할 때가 있습니다. 그럴떄 사용하는게 세그먼트 트리 비츠입니다. 다음으로는 세그먼트 트리 비츠를 알아보겠습니다.