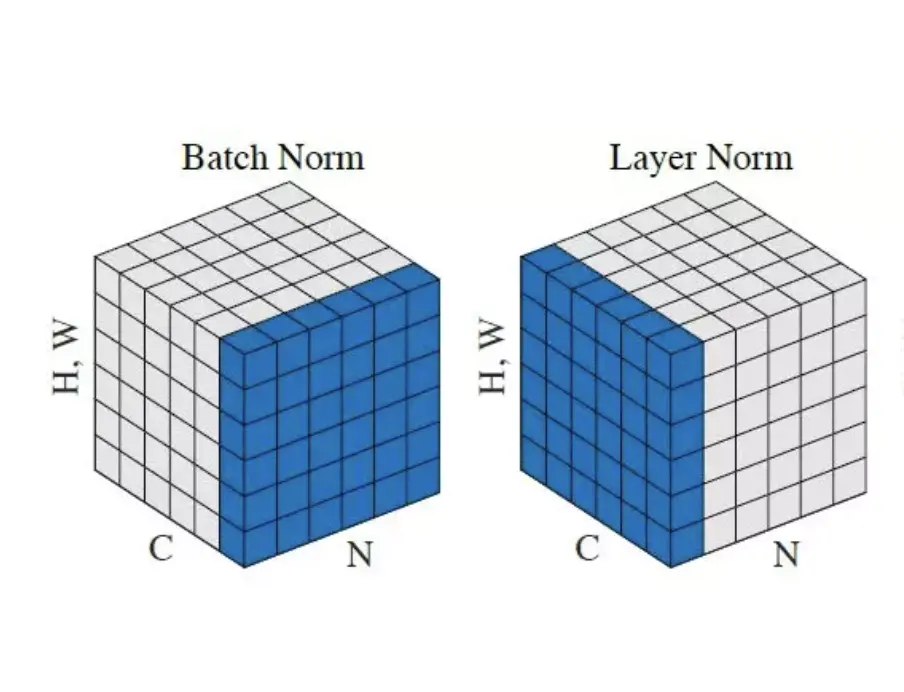
개요
레이어 정규화(Layer Normalization, LN)은 배치 정규화(Batch Normalization, BN)과 비슷하게 신경망 내부에서 정규화를 진행하는 방법입니다. 요즘 많이 연구되는 텍스트 생성과 같은 테스크에 주로 사용되는 Transformer, RNN과 같은 시퀀스 모델에는 BN이 적용이 어려워 Layer Normalization 고안된 정규화 방법입니다.
BN의 한계
BN에 대한 자세한 내용은 이전 포스트에서 확인 가능합니다.
BN은 학습 안정화, 학습 시간 감소 등 여러 장점이 있는 정규화 방법이지만, RNN과 같은 시퀀스 모델에는 사용하기 어렵다는 큰 단점이 있습니다.
BN은 이름에서 알 수 있듯이 미니배치 단위로 정규화를 수행합니다.
RNN과 같은 레이어는 이전 상태를 hidden state로 다음 레이어로 넘겨 재사용하는 특징이 있습니다.
여기서 BN을 사용할때 문제가 발생합니다.
이전 셀의 입력에서 수행한 BN은 t 시점에 입력된 미니배치를 기준으로 정규화가 수행됩니다.
그 다음 셀에는 t+1 시점에서 입력된 미니배치를 기준으로 정규화를 진행합니다.
그러나 t 와 t+1 시점의 배치는 들어온 입력값이 다르기 때문에 다른 정규화 결과를 가집니다.
이 상황에서 t+1 셀에서는 이전 셀에서 입력된 hidden state도 학습에 사용합니다.
이는 연속된 데이터지만 시점에 따라 분포를 다르게 만들어 데이터의 일관성을 깨뜨리는 문제를 발생시킵니다.
그래서 배치 단위가 아닌 샘플의 특징 차원을 기준으로 정규화 하는 LN이 고안되게 되었습니다. 위 그림에 차이가 잘 표현되어 있습니다.
계산 과정
BN과 다르게 특징차원 단위로 정규화 한다는 차이점 말고는 계산 과정 식 자체는 정규화이기 때문에 BN과 동일합니다.
\[\mu = \frac{1}{D}\sum_{d=1}^{D} x_d\] \[\sigma^2 = \frac{1}{D}\sum_{d=1}^{D} (x_d - \mu)^2\] \[\hat{x}_d = \frac{x_d - \mu}{\sqrt{\sigma^2 + \epsilon}}\]특징백터의 평균과 분산을 구한 뒤, 평균 0, 분산 1로 정규화를 진행합니다.
\[y_d = \gamma_d \cdot \hat{x}_d + \beta_d\]정규화 된 값에 \(\gamma_d\)를 곱하고 \(\beta_d\)를 더해 최종 출력 값을 만듭니다. BN과 마찬가지로 \(\gamma_d\)와 \(\beta_d\)는 학습 가능한 변수입니다. \(\gamma_d\)와 \(\beta_d\)값을 조정하여 네트워크가 필요한 분포로 조정을 진행합니다.
LN은 BN과 다르게 running mean/var가 따로 있지 않습니다. BN은 배치 사이즈에 따라 정규화 효과가 크게 달라져서 작은 배치로 진행되는 추론에 사용할 평균과 분산을 계산했다가 추론에 사용했지만, LN은 특징백터 단위로 정규화 되기때문에 배치사이즈에 영향을 받지 않습니다. 그래서 따로 평균과 분산을 저장했다가 사용할 필요가 없습니다.