[선형대수] 유클리드 벡터공간 - 벡터

기하학적 벡터

물리공간에서 벡터를 표현할 때 화살표로 표현한다. 이때 화살표의 방향은 벡터의 방향, 화살표의 크기는 벡터의 크기를 나타낸다. 벡터는 방향과 크기에 의해 결정되므로 방향과 크기만 같으면 두 벡터는 같다.

백터가 시작되는 지점을 시점, 벡터가 끝나는 지점을 종점이라고 한다. 시점이 \(A\), 종점이 \(B\)인 벡터 \(v\)를 \(v = \overrightarrow{AB}\) 로 표현한다. 시점과 종점이 같은 벡터는 영벡터이다.

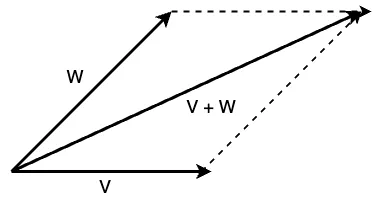
벡터 덧셈

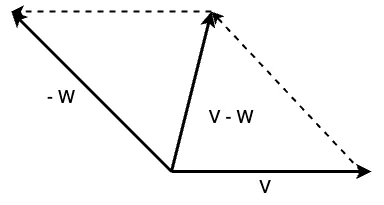
벡터 뺄셈

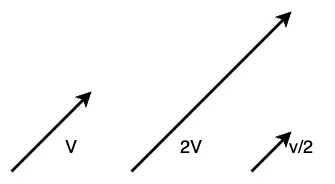
스칼라 곱셈

벡터의 동일 직선상과 평행

한 벡터의 스칼라배는 같은 직선상(collinear)에 놓인다. 동일 직선상에 놓인 벡터중 하나를 평행이동하면 이동한 벡터는 동일 직선상에 있던 다른 벡터와 절대 만나지 않으므로 평행(parallel)하다고 한다.

좌표계에서의 벡터

좌표계에서는 원점을 기준으로 각 위치를 표현하는 숫자로 표현된다. 예를들어 2차원 벡터는 \(v = (v_{1}, v_{2})\) 로 종점의 위치가 표현된다. 이를 백터의 성분(component)라고 부른다. 두 벡터의 성분이 모두 같으면 두 벡터는 동일한 벡터이다.

시점이 원점이 아닌 벡터

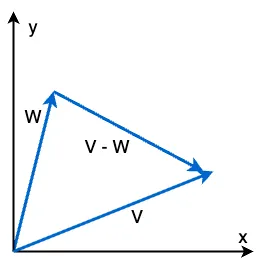
시점이 원점이 아닌 벡터는 시점이 원점인 두 벡터로 표현이 가능하다.

위 예제에서 \(v = (v_{1}, v_{2})\) 와 \(w = (w_{1}, w_{2})\) 라고 할 때, 시점이 원점이 아닌 벡터는 \(v - w = (v_{1} - w_{1}, v_{2} - w_{2})\) 로 표현이 가능하다.

백터 성잘

1. \(u + v = v + u\)
2. \((u + v) + w = v + (u + w)\)
3. \(u + 0 = 0 + u = u\)
4. \(u + (-u) = 0\)
5. \(k(u + v) = ku + kv\)
6. \((k + m)u = ku + mu\)
7. \(k(mu) = (km)u\)
8. \(1u = u\)