개요
활성화 함수(Activation Function)는 신경망에서 뉴런이 입력을 받아 출력으로 보낼 때 적용하는 비선형 함수입니다. 활성화 함수를 적용하여 비선형성을 주어 복잡한 문제를 학습할 수 있도록 합니다.
활성화 함수 종류
활성화 함수는 목적, 데이터 특성에 따라 다양한 함수를 사용합니다.
Sigmoid
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]시그모이드는 값을 0~1 사이로 압축하는 함수입니다. 음수 값이 클 수록 0에 가깝고, 양수 값이 클 수록 1에 가깝습니다. 그래서 0또는 1로 이진 분류하는 문제의 최종 출력으로 사용합니다.
하지만 기울기 소멸(Gradient Vanishing) 문제에 취약합니다. 시그모이드를 여러번 거치면 값이 점차 작아져 정보가 소실되는 포화(saturated)문제가 발생합니다.
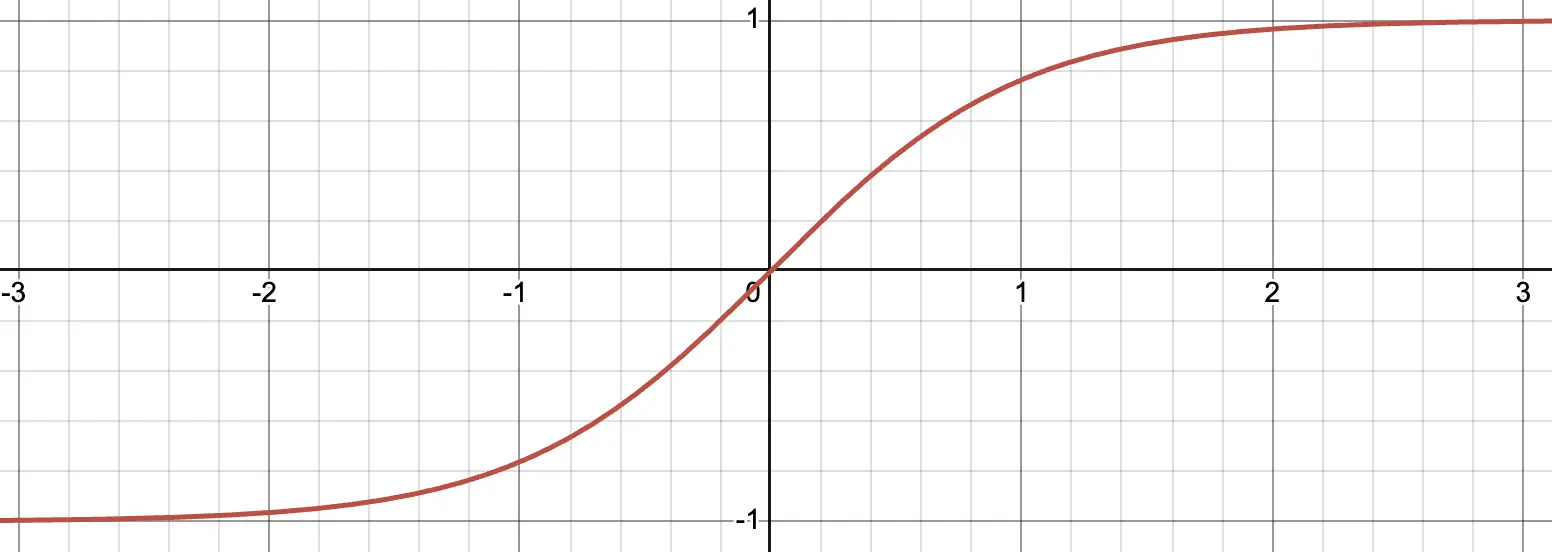
Tanh
\[\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]tanh는 시그모이드와 비슷하지만, -1~1 사이로 압축하는 함수입니다.
범위를 늘려 기울기 소실 문제를 완화했지만, 여전히 기울기 소실에 취약하다는 단점이 있습니다.
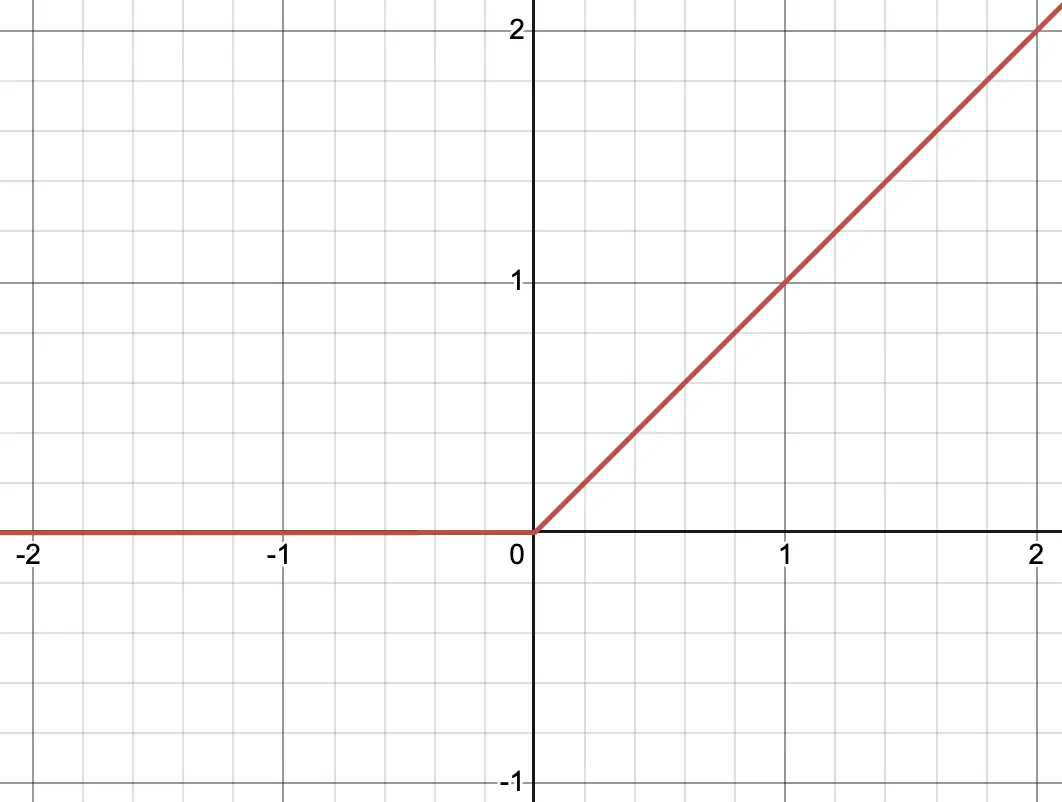
ReLU
\[f(x) = \max(0, x)\]ReLU는 0 이하의 입력은 모두 0으로, 0 보다 큰 입력은 모두 그대로 출력하는 함수입니다. 양의 입력일 때 입력 그대로를 출력하므로 sigmoid, tanh가 가지고 있던 포화(saturated)문제가 완화되어 기울기 소실 문제를 완화할 수 있습니다. 그리고 다른 함수와 달리 exp 연산이 없기때문에 연산 속도도 더욱 빠르다고 합니다.
그러나 relu 함수도 Dying ReLU 문제라는 단점이 있습니다.
ReLU는 0 이하는 모두 0으로 출력하기 때문에, 특정 뉴런이 항상 0만 출력하게 되는 죽은 뉴런(Dead Neuron)이 되는 현상이 발생할 수 있습니다.
죽은 뉴런은 항상 0만 출력하기 때문에 학습에 도움이 되지 않을 수 있습니다.
다만 정보를 찾다보니 이 현상이 오히려 일반화에 도움이 된다는 내용이 있어서 정말 단점인지는 조금 더 찾아봐야 할 것 같습니다.
관련 내용은 따로 분리하여 포스팅 하겠습니다.
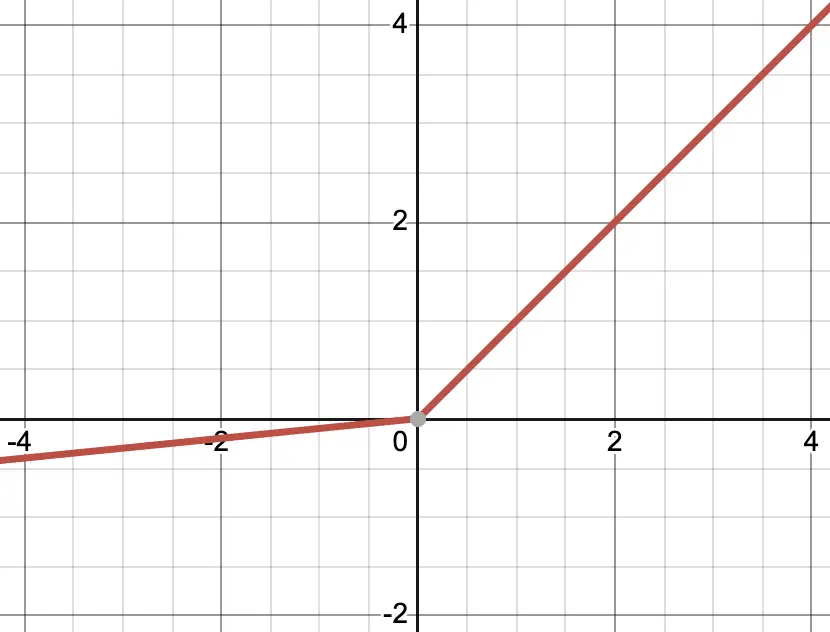
Leaky ReLU
\[f(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{if } x \leq 0 \end{cases}\]Leaky ReLU는 음수 영역에도 작은 기울기를 줘 Dead Neuron 문제를 방지하는 함수입니다. 이때 기울기는 임의로 설정이 가능한데, Pytorch의 기본 값은 0.01 입니다.
Softmax
\[f(x_i) = \frac{e^{x_i}}{\sum_j e^{x_j}}\]SoftMax는 여러 입력의 합을 1이 되도록 조정하는 함수입니다. 주로 분류 문제에서 여러 클래스의 확률 분포를 계산할 때 사용됩니다. 그래서 중간층에서는 활용하지 않고, 주로 마지막 출력층에서 활용됩니다.
이 외에도 GeLU, Swish 등 다양한 활성화 함수가 존재합니다. 데이터, 모델의 특징에 맞는 활성화 함수를 사용하여 좋은 성능을 낼 수 있도록 해야합니다.